Korrelation in Excel berechnen: Ihre Anleitung

Mit Microsoft Excel können Sie mehr als nur Tabellenkalkulationen erstellen – Sie können die Software auch verwenden, um wichtige Funktionen zu berechnen, wie z. B. die Beziehung zwischen zwei Variablen. Diese als Korrelationskoeffizient bekannte Metrik ist nützlich, um die Auswirkungen eines Vorgangs auf einen anderen zu messen, um den Geschäftsbetrieb zu informieren.

Sie sind sich Ihrer Excel-Kenntnisse nicht sicher? Kein Problem. So berechnen – und verstehen – Sie den Korrelationskoeffizienten in Excel.

Ein Korrelationskoeffizient von +1 weist auf eine „perfekte positive Korrelation“ hin, was bedeutet, dass die Variable Y mit der gleichen Rate zunimmt, wenn die Variable X zunimmt. Ein Korrelationswert von -1 ist hingegen eine „perfekte negative Korrelation“, was bedeutet, dass die Variable Y mit der gleichen Rate abnimmt, wenn die Variable X zunimmt. Die Korrelationsanalyse kann auch Ergebnisse irgendwo zwischen -1 und +1 zurückgeben, was darauf hinweist, dass sich Variablen mit ähnlichen, aber nicht identischen Raten ändern.

Korrelationswerte können Unternehmen dabei helfen, die Auswirkungen bestimmter Aktionen auf andere Aktionen zu bewerten. Beispielsweise können Unternehmen feststellen, dass mit steigenden Ausgaben für Social-Media-Marketing auch die Kundenbindung steigt, was darauf hindeutet, dass mehr Ausgaben sinnvoll sein könnten.

Oder sie stellen fest, dass bestimmte Werbekampagnen zu einer korrelierten Abnahme der Kundenbindung führen, was wiederum auf die Notwendigkeit einer Neubewertung der aktuellen Bemühungen hindeutet. Die Entdeckung, dass Variablen nicht korrelieren, kann ebenfalls wertvoll sein; Während der gesunde Menschenverstand vermuten lässt, dass eine neue Funktion oder ein neues Feature in Ihrem Produkt mit einem erhöhten Engagement korrelieren würde, hat dies möglicherweise keine messbaren Auswirkungen. Die Korrelationsanalyse ermöglicht es Unternehmen, diese Beziehung (oder deren Fehlen) zu erkennen und fundierte strategische Entscheidungen zu treffen.

Wie berechnet man also den Korrekturkoeffizienten in Excel? Einfach! Folge diesen Schritten:

1. Öffnen Sie Excel.

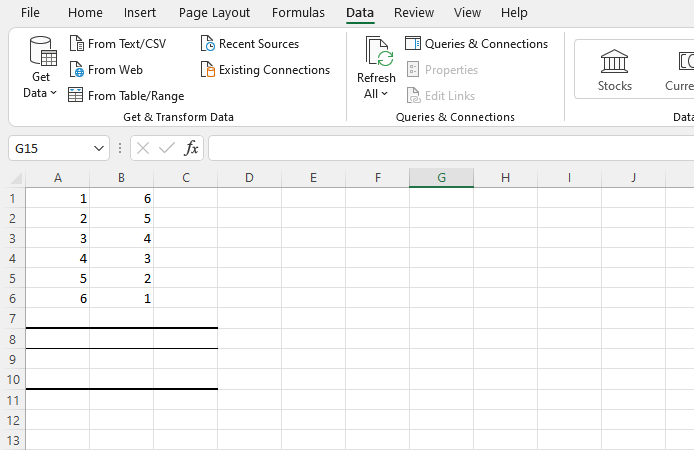
Schritt eins: Öffnen Sie Excel und erstellen Sie ein neues Arbeitsblatt für Ihre korrelierten Variablendaten. Geben Sie die Datenpunkte Ihrer ersten Variablen in Spalte A und Ihrer zweiten Variablen in Spalte B ein. Sie können auch zusätzliche Variablen in den Spalten C, D, E usw. hinzufügen. Excel liefert für jede einen Korrelationskoeffizienten.

Im folgenden Beispiel haben wir sechs Datenzeilen in Spalte A und sechs in Spalte B eingegeben.

2. Installieren Sie das Analysis Toolpak.

Next Up? Wenn Sie es nicht haben, installieren Sie das Excel Analysis Toolpak.

Wählen Sie „Datei“ und dann „Optionen“ und Sie sehen diesen Bildschirm:

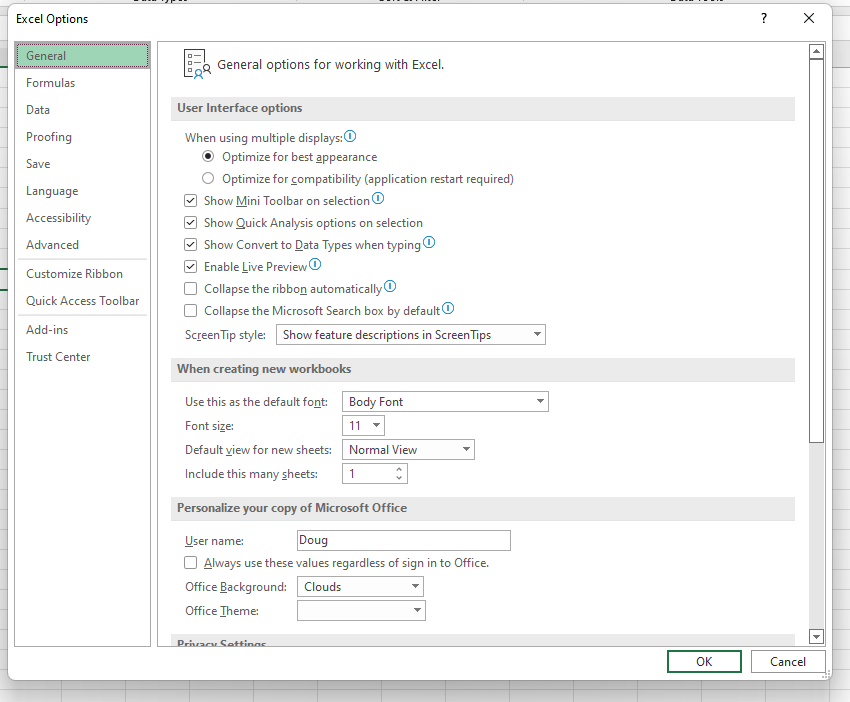
Wählen Sie „Add-Ins“ und klicken Sie dann auf „Los“.

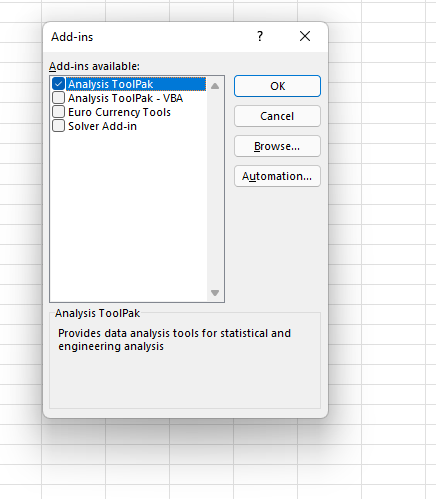
Aktivieren Sie nun das Kontrollkästchen „Analysis ToolPak“ und klicken Sie auf „Ok“.

3. Wählen Sie „Daten“ aus dem Menü der oberen Leiste.

Sobald Sie das ToolPak installiert haben, wählen Sie „Daten“ aus dem oberen Menü der Excel-Leiste. Dieser stellt Ihnen ein Untermenü zur Verfügung, das vielfältige Analysemöglichkeiten für Ihre Daten enthält.

4. Wählen Sie oben rechts „Datenanalyse“ aus.

Suchen Sie nun in der oberen rechten Ecke nach „Datenanalyse“ und klicken Sie darauf, um diesen Bildschirm zu erhalten:

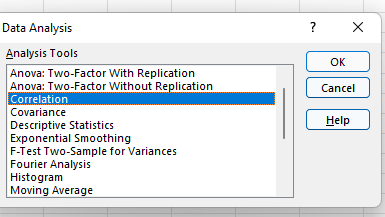
5. Wählen Sie Korrelation.

Wählen Sie Korrelation aus dem Menü und klicken Sie auf „OK“.

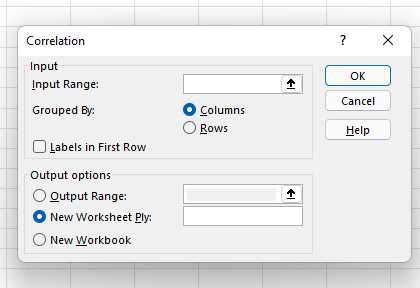
6. Definieren Sie Ihren Datenbereich und Ihre Ausgabe.

Definieren Sie nun Ihren Datenbereich und Ihre Ausgabe. Sie können einfach mit der linken Maustaste klicken und Ihren Cursor über die Daten ziehen, die Sie auswählen möchten, und sie werden automatisch in das Korrelationsfeld eingetragen. Wählen Sie abschließend einen Ausgabebereich für Ihre Korrelationsdaten aus – wir haben uns für A8 entschieden. Klicken Sie dann auf „Ok“.

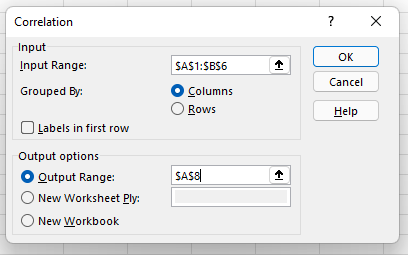
7. Bewerten Sie Ihren Korrelationskoeffizienten.

Ihre Korrelationsergebnisse werden nun angezeigt. In unserem Beispiel haben die Werte in Spalte 1 und Spalte 2 eine perfekte negative Korrelation; Wenn einer steigt, sinkt der andere mit der gleichen Geschwindigkeit.

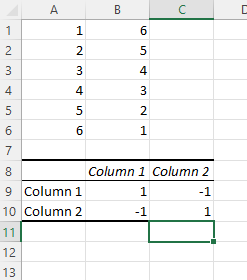
Die Excel-Korrelationsmatrix

Excel-Korrelationsergebnisse werden auch als Excel-Korrelationsmatrix bezeichnet. Im obigen Beispiel haben unsere beiden Datenspalten eine perfekte Korrekturmatrix von 1 und -1 erzeugt. Aber was passiert, wenn wir eine Korrelationsmatrix mit einem weniger idealen Datensatz erstellen?

Hier unsere Daten:

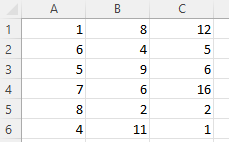
Und hier ist die Matrix:

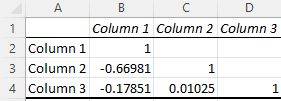
Zelle C4 in der Matrix gibt uns die Korrelation zwischen Spalte 3 und Spalte 2, die sehr schwache 0,01025 ist, während Spalte 1 und Spalte 3 eine stärkere negative Korrelation von -0,17851 ergeben. Die mit Abstand stärkste Korrelation besteht jedoch zwischen Spalte 1 und Spalte 2 bei -0,66891.

Was bedeutet das in der Praxis? Nehmen wir an, wir untersuchen die Auswirkungen bestimmter Aktionen auf die Wirksamkeit einer Social-Media-Kampagne, wobei Spalte 1 die Anzahl der Besucher darstellt, die sich durch soziale Anzeigen klicken, und Spalte 2 und 3 zwei verschiedene Marketing-Slogans darstellen. Die Korrelationsmatrix zeigt eine starke negative Korrelation zwischen den Spalten 1 und 2, was darauf hindeutet, dass die Version des Slogans in Spalte 2 die allgemeine Benutzerinteraktion deutlich verringerte, während Spalte 3 nur einen leichten Rückgang bewirkte.

Das regelmäßige Erstellen von Excel-Matrizen kann Unternehmen dabei helfen, die Auswirkungen einer Variablen auf eine andere besser zu verstehen und festzustellen, welche negativen oder positiven Auswirkungen (falls vorhanden) bestehen können.

Die Excel-Korrelationsformel

Wenn Sie die Korrelationsformel lieber selbst eingeben möchten, ist das auch eine Option. So sieht es aus:

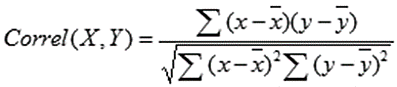
X und Y sind Ihre Messungen, ∑ ist die Summe, und X und Y mit den Balken darüber geben den Mittelwert der Messungen an. Sie würden es wie folgt berechnen:

• Berechnen Sie die Summe der Variablen X minus dem Mittelwert von X.
• Berechnen Sie die Summe der Variablen Y minus dem Mittelwert von Y.
• Multiplizieren Sie diese beiden Ergebnisse und legen Sie diese Zahl beiseite (dies ist das erste Ergebnis).
• Quadrieren Sie die Summe von X minus dem Mittelwert von X. Quadrieren Sie die Summe von Y minus dem Mittelwert von Y. Multiplizieren Sie diese beiden Zahlen.
• Ziehen Sie die Quadratwurzel (das ist das zweite Ergebnis).
• Teilen Sie das erste Ergebnis durch das zweite Ergebnis.
• Sie erhalten den Korrelationskoeffizienten.

Einfach richtig? Ja und nein. Während das Einfügen der Zahlen nicht kompliziert ist, macht es oft mehr Mühe als es wert ist, diese Formel zu erstellen und zu verwalten. Das integrierte Excel Toolpak ist oft eine einfachere (und schnellere) Möglichkeit, Koeffizienten zu lokalisieren und wichtige Beziehungen zu entdecken.

Korrelation ≠ Nicht Kausalität

Kein Artikel über Korrelation ist vollständig ohne die Erwähnung, dass dies nicht gleich Kausalität ist. Mit anderen Worten, nur weil zwei Variablen zusammen steigen oder fallen, heißt das nicht, dass eine Variable die Ursache für den Anstieg oder Rückgang der anderen Variable ist.

Betrachten Sie einige sehr seltsame Beispiele.

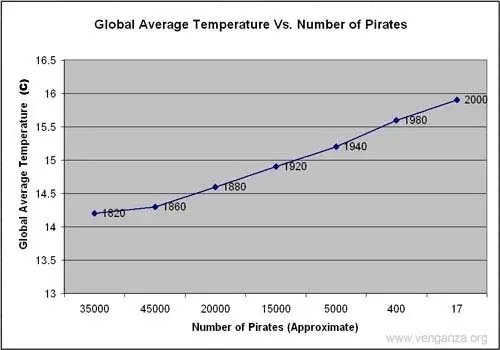
Dieses Bild zeigt eine nahezu perfekte negative Korrelation zwischen der Anzahl der Piraten und der globalen Durchschnittstemperatur – als Piraten seltener wurden, stieg die Durchschnittstemperatur.

Das Problem? Obwohl diese beiden Variablen korreliert sind, gibt es keinen kausalen Zusammenhang zwischen den beiden; Höhere Temperaturen reduzierten die Piratenpopulation nicht und weniger Piraten verursachten keine globale Erwärmung.

Korrelation ist zwar ein leistungsfähiges Werkzeug, zeigt aber nur die Richtung der Zunahme oder Abnahme zwischen zwei Variablen an – nicht die Ursache dieser Zunahme oder Abnahme. Um kausale Zusammenhänge zu entdecken, müssen Unternehmen eine Variable erhöhen oder verringern und die Auswirkungen beobachten. Wenn beispielsweise die Korrelation zeigt, dass die Kundenbindung mit den Ausgaben für soziale Medien steigt, lohnt es sich, sich für eine leichte Erhöhung der Ausgaben zu entscheiden, gefolgt von einer Messung der Ergebnisse. Wenn mehr Ausgaben direkt zu mehr Engagement führen, ist die Verbindung sowohl korreliert als auch kausal. Wenn nicht, kann es einen (oder mehrere) Faktoren geben, die den Anstieg beider Variablen untermauern.

Mit den Korrelationen Schritt halten

Excel-Korrelationen bieten einen soliden Ausgangspunkt für die Entwicklung von Marketing-, Vertriebs- und Ausgabenstrategien, aber sie erzählen nicht die ganze Geschichte. Daher lohnt es sich, die in Excel integrierten Datenanalyseoptionen zu verwenden, um die Korrelation zwischen zwei Variablen schnell zu bewerten und diese Daten als Ausgangspunkt für tiefergehende Analysen zu verwenden.