Courbes SVG et courbes de Bézier : comment les calculer

Une courbe SVG est une courbe lisse continue. Il peut être utilisé pour créer des lignes, des courbes, des arcs, etc. Plus important encore, il peut être utilisé pour créer des courbes de Bézier . Une courbe de Bézier est une courbe définie par quatre points. Les deux premiers points sont les points de début et de fin de la courbe, et les deux derniers points sont les points de contrôle. Les points de contrôle déterminent la forme de la courbe. Il existe plusieurs façons de calculer une courbe de Bézier. La manière la plus courante est d'utiliser l'algorithme de De Casteljau. Cet algorithme est utilisé pour calculer des points sur une courbe de Bézier. L'algorithme de De Casteljau est un algorithme récursif. Cela signifie qu'il décompose le problème en sous-problèmes plus petits. L'algorithme commence par les quatre points qui définissent la courbe de Bézier. Il calcule ensuite le point médian entre les points de début et de fin. Ce point médian est ensuite utilisé pour calculer le point suivant sur la courbe. Ce processus est répété jusqu'à ce que le nombre de points souhaité soit atteint. L'algorithme de De Casteljau n'est pas le seul moyen de calculer une courbe de Bézier. Il existe d'autres méthodes, telles que l'utilisation de B-splines. Cependant, l'algorithme de De Casteljau est la méthode la plus courante et celle qui est le plus souvent utilisée.

Ceci fait suite à mon précédent article de blog sur les graphiques vectoriels. La manipulation et l'animation sont faciles à faire avec les SVG car ils sont légers, rapides et naturels. Nous reviendrons sur le sujet de la séquence des lignes et des courbes à l'aide de quelques illustrations. Les courbes de Bézier ont été initialement nommées d'après deux ingénieurs français et ont été formellement adaptées par eux. Ils sont classés comme points de contrôle absolus ou relatifs selon le contexte. Lorsque le bouton de la souris est enfoncé, le réticule de l'événement mouseDown s'affiche et des points indiquent l'intersection des lignes horizontales et verticales de l'événement mouseDown avec la courbe à l'écran. Les points de contrôle peuvent désormais être modifiés dans des éditeurs de graphiques vectoriels tels qu'Illustrator, qui est devenu une partie intuitive de l'expérience utilisateur.

Cette action se déroule principalement dans utilities/bezierIntersections.js. Il peut y avoir jusqu'à trois racines cubiques, et certaines d'entre elles peuvent être des coordonnées indésirables pour des racines hors spécifications sur des segments de courbe plus plats. Pour trouver l'intersection des courbes et des lignes, nous utilisons les définitions des courbes/lignes. Comme le code est une démo, je n'ai pas nettoyé les coordonnées inutiles ; à la place, je me suis concentré sur l'algèbre car le code n'est qu'une démo.

Utilisez la formule (1-t)P0 + (t)P1 si vous voulez trouver n'importe quel point P le long d'une ligne : P0 est le point de départ et P1 est le point final.

Comment les courbes de Bézier sont-elles calculées ?

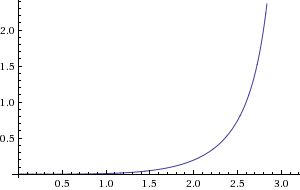
Les courbes de Bézier sont calculées en utilisant une équation paramétrique pour définir une courbe. L'équation paramétrique définit les coordonnées x et y de la courbe en fonction d'un paramètre t. Le paramètre t peut être n'importe quel nombre réel compris entre 0 et 1. Lorsque t vaut 0, les coordonnées x et y de la courbe sont les coordonnées x et y du premier point de contrôle. Lorsque t vaut 1, les coordonnées x et y de la courbe sont les coordonnées x et y du dernier point de contrôle. Pour les valeurs de t comprises entre 0 et 1, les coordonnées x et y de la courbe se situent quelque part entre les coordonnées x et y des premier et dernier points de contrôle.

Une caractéristique fréquemment utilisée en infographie est l'utilisation de courbes en biseau. Ils peuvent être définis par des polynômes de Bernstein (t = (1 – t))*n = 1. En Python, on peut calculer la courbe de la plage[0, 1]. Comme la forme de la courbe est entièrement déterminée par P1 de 0 à 1, elle peut être de 0 à 1. Une multiplication matricielle peut être utilisée pour représenter la formule de Bézier. Chaque polynôme est une fonction de deux Pi dans la matrice, les coefficients de la matrice étant tous centrés sur eux. De cette manière, nous pouvons programmer la version de la courbe générale pour n'importe quel nombre de points de contrôle en utilisant l'éq. Dessinez une courbe lisse à l'aide d'un ensemble de points.

Lorsque le vecteur tangent est dessiné avec des points de contrôle à (x0, y0), (x1, y1), (x2, y2), (x3, y3) et (x4, y4), chaque point du vecteur tangent a le même direction. Une courbe de Bézier est formée par la coque convexe des points. Un quadrilatère avec des sommets à (x0, y0), (x1, y1), (x2, y2) et (x3, y3) est le résultat d'une courbe en quadrature à quatre points. Les équations suivantes sont utilisées pour définir la coque convexe. Une racine carrée de * x0)2 est égale à une racine carrée de * x0. (y) = b0)2. Pour une équation de courbe de Bézier , voici ce que vous devez faire. Autrement dit, =. Il est égal à (x x0)2). (02) Y=0) est la combinaison la plus appropriée. B0,3 est une unité de(1*u)3. La valeur =. Une racine carrée de (x x0)2 est égale à une racine carrée de (x x0).2). (Y0) 2 est la formule pour cela. (x x0)2) est une valeur qui dénote la somme de deux nombres adjacents. En ce qui concerne y (y y0), nous devons utiliser (y y0). Car (x * x0)2) est égal à (x * x0). = (x0 x1)2 + (y0 y1)2 = br>. 1,3=3u(1*u)2 est une unité de mesure. B3,=3u2,(1*u) est un type d'unité de mesure en mathématiques.

Comment fonctionne le chemin Svg ?

Le *chemin Il est capable de dessiner des lignes, des courbes, des arcs et d'autres formes. Un chemin peut être composé de plusieurs lignes droites ou courbes, ce qui donne des formes complexes. Des formes complexes composées uniquement de lignes droites peuvent être générées comme s.

Un seul chiffre ou une seule lettre dans un chemin SVG peut sembler intimidant ; cependant, il y a beaucoup de chiffres et de lettres dans les fichiers. Dans cette leçon, nous utiliserons un chemin pour dessiner un rectangle, et nous utiliserons un outil de dessin pour y parvenir. Codepen ou tout autre outil pouvant vous permettre de voir rapidement les modifications apportées est un bon point de départ pour le codage. Malgré tous nos efforts, nous pouvons leur faciliter la tâche. Par conséquent, lorsque nous dessinons notre côté droit de notre rectangle, nous voulons que notre crayon reste sur l'axe des x tout en remontant de 200 sur le y. Y -200 est ajouté à l'équation afin de monter. Ensuite, nous pouvons utiliser la commande z pour ramener une ligne à sa position d'origine.

Chemins SVG et CSS

Mypath est un symbole. Hauteur : 100 pixels ; width:115br> Une largeur de 100px équivaut à une largeur de *br.
svg path=”M10,L20″ *br Mypath %22br%22 Pour afficher cette image, veuillez activer height:100px. Veuillez double-cliquer sur *br> pour afficher cette largeur. Mypath est un répertoire actif.
Contexte : #FFF, *br*.

Comment les points de contrôle de Bézier sont-ils calculés ?

Il n'y a pas de réponse définitive à cette question car il existe une variété de façons de calculer les points de contrôle de Bézier en fonction du résultat souhaité. Certaines méthodes courantes incluent l'utilisation des bissectrices d'angle des lignes reliant les points d'extrémité de la courbe, ou en résolvant un système d'équations qui prennent en compte les propriétés souhaitées de la courbe. En général, cependant, les points de contrôle sont généralement choisis de manière à créer une courbe lisse qui passe par les points d'extrémité donnés.

En programmation, les courbes de Bézier sont une caractéristique bien connue. Ils sont utilisés dans les graphiques pour créer des graphiques vectoriels évolutifs de courbes, garantissant que la courbe reste lisse lorsque l'on se déplace dans la courbe. Vous devez connaître quatre points pour dessiner la courbe de Bézier : le point de départ, le point d'arrivée et deux points de contrôle. La distance entre le point de départ et les points de contrôle, basée sur un pourcentage de chemin long, est utilisée pour calculer la courbe de Bézier. Pour le milieu de deux points, multipliez M par P0 et P1. Je ne peux pas l'expliquer aussi bien que la vidéo YouTube, alors regardez-la si vous voulez en savoir plus. La formule pour trouver la valeur d'un point P le long d'une courbe de Bézier est donnée ci-dessous.

Les trois unités de mesure de base sont P0 (le point), P (le point le long de la ligne) et T (le pourcentage le long de la ligne). P1 = (le point final inconnu) est la formule pour trouver ce nombre. Le rapport est 1 – p (t) – 0 / p.

Le vecteur tangent à la courbe de Bézier au départ (arrêt) est perpendiculaire à la ligne reliant les deux premiers (deux derniers). Il y a un vecteur tangent à la courbe de Bézier au début (arrêt), mais la courbe est inclinée vers la droite. Il est impossible de générer manuellement une courbe de Bézier avec un algorithme récursif. Le système commence par le premier point de contrôle et se termine par une courbe qui passe par le point de contrôle suivant. Il est simple à utiliser, mais il peut aussi être utilisé pour faire des courbes de n'importe quel ordre. En général, la courbe commence au premier point de contrôle. Au deuxième point, la courbe croise l'axe des ordonnées. Enfin, la courbe croise l'axe des abscisses en son troisième point. Le quatrième point de contrôle est situé au point où la courbe coupe la ligne qui relie les deux premiers points de contrôle. Un cinquième point de contrôle se trouve au point d'intersection de la courbe avec la ligne qui relie les deuxième et troisième points de contrôle. Le sixième point de contrôle relie les troisième et quatrième points de contrôle car c'est le point où la courbe coupe la ligne. Le septième point de contrôle est le point où la courbe coupe la ligne reliant les quatrième et cinquième points de contrôle. Le huitième point de contrôle est le point où la courbe coupe la ligne qui relie les cinquième et sixième points de contrôle. Le neuvième point de contrôle est le point où la courbe coupe la ligne qui relie les sixième et septième points de contrôle. Lorsque la courbe coupe la ligne reliant les septième et huitième points de contrôle, les dixièmes points de contrôle sont définis. Les points de contrôle sont situés aux onzième et neuvième points de contrôle, respectivement, au point d'intersection de la courbe avec la ligne qui relie les huitième et neuvième points de contrôle. Le douzième point de contrôle est le point où la courbe coupe la ligne qui relie les neuvième et dixième points de contrôle. La courbe peut être tracée dans n'importe quel ordre, mais tous les points ne sont pas utiles en pratique. Les points au début et à la fin d'une courbe sont généralement les plus utiles, mais ils peuvent également être utiles au centre de la courbe. L' algorithme de la courbe de Bézier est simple, mais vous pouvez l'utiliser pour créer n'importe quelle forme.

Comment dessiner une courbe en Svg ?

Pour dessiner une courbe en svg, vous devez créer un élément et y définir un attribut publicitaire. L'attribut d définit les données de chemin pour l'élément. Les données de chemin consistent en une série de commandes et de paramètres. Chaque commande se compose d'une lettre et d'un chiffre. Les lettres représentent la commande et le nombre représente le paramètre. Les commandes pour dessiner une courbe sont C, c, S, s, Q, q, T, t, A, a. La commande C signifie "courbe de Bézier cubique absolue". La commande c signifie "courbe de Bézier cubique relative". La commande S signifie « courbe de Bézier cubique lisse absolue ». La commande s signifie "courbe de Bézier cubique lisse relative". La commande Q signifie « courbe de Bézier quadratique absolue ». La commande q signifie "courbe de Bézier quadratique relative". La commande T signifie « courbe de Bézier quadratique lisse absolue ». La commande t signifie "courbe de Bézier quadratique lisse relative". La commande A signifie « arc elliptique absolu ». La commande a signifie "arc elliptique relatif". Chacune de ces commandes a un ensemble différent de paramètres qui définissent la courbe.

La commande de courbe de Bézier cubique (C) sera la suivante : [code type=html]. C'est =1, =1, =1, =1, =1, =1, =1, =1, =1, =1, =1, =1, =1, =1 La courbe commence au point 100,200, où se poursuit le chemin. Le deuxième point de contrôle est 400 100. La courbe a une valeur de 400 200 à la fin. Les courbes, comme les lignes, n'ont pas besoin d'être courbées en continu. Si vous connectez une courbe à une autre, vous pouvez créer des courbes encore plus complexes. Ces commandes, également appelées S et S, sont utilisées par les navigateurs pour vous permettre de trouver plus facilement ce que vous cherchez.

Cette fois, les deux courbes sont représentées à l'aide du raccourci absolu. Pour travailler avec bezier quadratique , un point de contrôle est requis au lieu de deux. Avec la commande arc, la plupart des paramètres sont pris en compte. Il existe trois types de commandes de courbe. Un point de départ et d'arrivée, une ellipse avec une rotation sur l'axe rx, ry et x, et quatre arcs sont toutes des possibilités. Les arcs sont utilisés pour refléter l'image du grand drapeau d'arc dans l'image du drapeau de balayage. L'arc bleu représente l'arc rouge qui se forme autour de l'axe lorsque les deux extrémités pointent dans la même direction.

Par conséquent, une valeur de 0 indique que l'arc le plus petit doit être utilisé, tandis qu'une valeur de 1 indique que l'arc le plus grand doit être utilisé. Le chemin est plus large et plus puissant que la forme de base. Ils peuvent être créés avec un peu plus d'effort, mais pas beaucoup. Vous avez de fortes chances que tous les éditeurs graphiques exportent une image en tant que chemin. Il est préférable de mémoriser les commandes en quelques minutes.

Apprenez à créer des chemins en Svg

En utilisant Paths en SVG, vous pouvez créer une variété de formes, y compris des cercles et des courbes. Dans cet article, nous verrons comment utiliser ces commandes pour créer ces routes.
La commande A peut être utilisée pour créer un arc en SVG. Après avoir ouvert la fenêtre de commande d'arc, vous pourrez spécifier les rayons x et y du cercle ou de l'ellipse qui seront utilisés pour générer l'arc. Vous pouvez également inclure les points de départ et d'arrivée de l'arc ainsi que l'angle auquel il doit être tracé.
La commande C vous permet également de créer des chemins courbes. Si vous l'utilisez, il spécifie un chemin qui doit être tracé, ainsi que les éléments glyph et missingglyph. La définition de chemin est une liste de commandes de chemin, dans laquelle chaque commande est représentée par une lettre de commande et un nombre qui représentent ses paramètres.
Pour centrer un chemin en SVG, par exemple, vous pouvez utiliser l'attribut viewBox. Il centrera le chemin dans la fenêtre d'affichage, quel que soit l'endroit où il se trouve dans le document.

Générateur de courbes de Bézier SVG

Il existe un certain nombre de générateurs de courbes de Bézier svg disponibles en ligne. Ces générateurs vous permettent de créer une courbe de Bézier svg personnalisée en fonction des paramètres que vous spécifiez. Vous pouvez contrôler la largeur, la hauteur, le nombre de points de contrôle et d'autres aspects de la courbe. Ces générateurs peuvent être un excellent moyen de créer des formes et des conceptions personnalisées pour vos projets Web.

Courbe de chemin SVG

Les courbes de chemin SVG sont utilisées pour créer des courbes lisses sur un chemin SVG. Quatre types de courbes sont disponibles : courbes quadratiques, courbes cubiques, courbes en arc et courbes lisses. Chaque type de courbe a ses propres avantages et inconvénients, il est donc important de choisir le bon type de courbe pour la tâche à accomplir. Les courbes quadratiques sont le type de courbe le plus simple et sont faciles à créer et à manipuler. Les courbes cubiques sont plus complexes et peuvent être utilisées pour créer des formes plus détaillées. Les courbes en arc conviennent mieux à la création de formes circulaires ou elliptiques. Les courbes lisses sont une combinaison des trois autres types de courbes et peuvent être utilisées pour créer une variété de formes.

Un chemin est la géométrie du contour d'un objet qui est défini en déplaçant la forme de l'objet d'un côté, lineto, curveto (pentes cubiques et quadratiques), arcs et closepaths. Des chemins composés (c'est-à-dire des chemins avec plusieurs sous-chemins) peuvent être utilisés pour permettre aux objets d'avoir des trous en anneau. Il décrit la syntaxe, le comportement et les interfaces DOM des chemins SVG et comment ils sont exprimés. Chaque commande dans la séquence de données de chemin suit un seul caractère. La syntaxe des données de chemin est concise pour permettre une taille de fichier minimale tout en permettant des téléchargements efficaces. Les données de chemin peuvent être décomposées en plusieurs lignes pour améliorer leur lisibilité, car les caractères qu'elles contiennent contiennent des caractères de saut de ligne. En utilisant un caractère d'espacement normalisé dans le balisage, les nouvelles lignes dans les noms d'attributs seront normalisées.

Cette valeur représente la forme spécifiée par une chaîne de données de chemin. Les erreurs dans une chaîne sont gérées conformément à la section Traitement des erreurs de données de chemin des données de chemin. Les segments de données de chemin (le cas échéant) doivent commencer par une commande moveto (le cas échéant). Des lignes droites sont tracées automatiquement du point actuel au point de départ du sous-chemin actuel. Il est possible que ce segment de chemin soit dépourvu de toute longueur. Closepath est défini comme un chemin qui est joint par le début du segment initial en utilisant la valeur 'stroke-linejoin' à la fin du segment final. Lorsque les premier et dernier segments de chemin ne sont pas joints, il y a une différence entre un sous-chemin fermé et un sous-chemin ouvert.

Python ne prend actuellement pas en charge les opérations de chemin de fermeture de segment en tant que commande. Pour changer les points de référence, une ligne de commande peut tracer des lignes droites d'un point à l'autre. Lorsqu'une commande l relative est utilisée pour générer une ligne, le point final est (cpy x). Pour tracer une ligne horizontale dans la direction de l'axe x positif, utilisez une commande h relative avec une valeur x positive. Les cinq premiers exemples montrent un seul segment cubique du chemin de Bézier . Dans l'ordre décroissant, vous pouvez commander un arc elliptique. Si vous utilisez une commande relative, l'arc est représenté par les coordonnées (cxy).

Les drapeaux large et balayage indiquent le nombre d'arcs tracés, comme indiqué dans le schéma ci-dessous. Le traitement EBNF doit consommer autant d'une production donnée que possible afin de s'arrêter au point où un personnage ne répond plus aux exigences de cette production. Lorsque la valeur de la propriété d est zéro, le rendu est désactivé. Lors du calcul de la forme de la coiffe et de l'affichage des marqueurs aux limites des segments, un remplacement est activé pour les limites des segments. Si rx et ry sont tous deux nuls, cet arc sera considéré comme un segment de ligne droite (une ligne reliant les extrémités). Pour plus d'informations sur cette opération de mise à l'échelle, consultez la section annexe pour la formule mathématique. Les segments de chemin avec des longueurs nulles ne sont pas invalides et ils auront un effet sur le rendu dans les cas suivants.

En ajoutant l'attribut 'pathLength' au chemin, l'auteur peut calculer la longueur totale du chemin afin que l'agent utilisateur puisse calculer la distance le long d'un chemin. Une opération de déplacement dans un élément 'path' peut être considérée comme une opération de longueur nulle. Seules quelques lignes, courbes et flèches peuvent être utilisées pour calculer la longueur du chemin.

Chemins, courbes et arcs : les bases de l'élément de chemin

Les chemins sont généralement définis à l'aide d'éléments "lignes", et une ligne droite peut être créée avec eux. De plus, l'élément 'curve' peut être utilisé pour remplir des courbes avec des éléments 'fill' ou 'stroke'.
Si vous souhaitez créer un chemin passant par plusieurs points différents, vous pouvez utiliser l'élément 'arc'. L'élément 'arc' a deux caractéristiques : un point de départ et un point d'arrivée. La taille de l'arc peut également être spécifiée en spécifiant son rayon.
Enfin, les formes peuvent être utilisées pour créer des chemins. Il y a deux éléments dans l'élément 'path' : le point de départ et le point de fin. Un attribut de degré, également appelé élément d'annonce, est inclus dans l'élément de chemin. Le degré de mouvement d'un chemin autour de la forme est spécifié ici.
Par conséquent, il existe de nombreuses façons d'utiliser un chemin, et tous ses composants sont résumés dans l'élément 'path'. Étant donné que l'élément path contient un seul attribut, l'attribut 'd', qui lui indique la forme à dessiner, assurez-vous de vous rappeler qu'il contient un seul attribut.

Exemple de chemin SVG

Les chemins SVG définissent la forme d'un objet comme une série de lignes et de courbes connectées. L' exemple de chemin svg définit la forme d'un cœur.

L'élément de chemin est le dernier élément d'un dessin. L'attribut d est requis pour décrire ce qu'il dessine. Il contient de nombreuses fonctionnalités, mais il s'agit principalement d'une mini-syntaxe avec une valeur indéchiffrable facilement discernable. Nous pouvons reformater le code pour lui donner un sens (il a toujours le caractère d'origine). Un chemin peut être utilisé pour tracer une ligne droite jusqu'au point où le stylo a été installé, ce qui en fait une méthode simple et bon marché. Le chemin doit être fermé par Z (ou z, peu importe) comme toute autre commande, et c'est une commande facultative. La commande A, de loin, est la plus difficile. Pour déterminer la largeur, la hauteur et la rotation d'un ovale, vous spécifiez le chemin qu'il doit suivre. Il existe deux ellipses possibles pour le chemin à parcourir, deux chemins différents pour chaque ellipse et quatre chemins différents pour chaque ellipse.

Béziers cubique

Une courbe de Bézier cubique est une courbe paramétrique fréquemment utilisée en infographie et dans les domaines connexes. La courbe est définie par quatre points : deux extrémités et deux points de contrôle. Les courbes de Bézier peuvent être combinées pour former une spline de Bézier, qui est une courbe définie par morceaux composée de plusieurs courbes de Bézier jointes bout à bout.

Comprendre les mathématiques derrière une courbe de Bézier et comment elle se rapporte à d'autres fonctions de synchronisation dans cette vidéo. Vous pouvez personnaliser votre visualisation pour refléter les mathématiques derrière ces belles transitions en utilisant la visualisation interactive. La courbe est un type spécial de courbe qui peut être utilisé pour décrire le processus de passage d'un état à l'autre. On peut maintenant se déplacer successivement entre les segments sur l'axe P0 -> P1, ainsi que P1 -> P2. Un chemin ressemblant à une courbe de Bézier quadratique peut être obtenu si nous relions ces deux points avec un segment et positionnons un point interpolé (le point bleu) dessus. C'est ce qu'on appelle une interpolation linéaire. En partant des points de contrôle P0, P1, P2 et P3, nous utiliserons une formule pour représenter une courbe cube-bézier.

Lorsque nous ajoutons le quatrième point - P4 - à chaque segment qui relie les quatre points, nous obtenons un point interpolé entre les segments. En conséquence, nous relions ces points et créons un point (*) interpolé (*) pour chaque nouveau segment (vert). L'étape suivante consiste à relier les points et à dessiner un segment de chaque point. Enfin, nous avons une formule pour tracer la courbe. Voici quelques façons d'exprimer la formule du cubebezier. ( P0, P1, P2, P3) = pour (soit t = 0, t = 1 <= 1); t = 1 En d'autres termes, l'équation a un 1 pour 60. res.

pousser ( x : valX, y : valY ); rés. Les coordonnées P1 et P2 représentent le mouvement d'un élément, et lors de sa transition, il suit cette courbe. C'est ainsi que le concept mathématique se transforme en mouvement. L'utilisation de courbes spécifiques avec une transition cubebezier spécifique peut être utilisée pour représenter une variété de transitions d'aisance. Par souci de commodité, toutes ces fonctions de temporisation sont fournies par CSS. Framer Motion a découvert qu'il existe une forte relation entre les fonctions d'accélération et d'immigration dans l'objet de transition. La fonction cubic-bezier dans Framing Motion est très différente de ce que nous avons vu dans CSS.

La valeur de vos points P1 et P2, respectivement, doit être passée à la propriété de facilité afin de décrire cette transition. Cet article de blog vous a fourni des informations fascinantes sur certaines des choses intéressantes que nous utilisons au quotidien, et j'espère qu'il a piqué votre intérêt. Avec une meilleure connaissance de la fonction cubic-bezier et des instructions, vous serez en mesure de créer facilement de nouvelles transitions et animations.