Menghitung Korelasi di Excel: Panduan Cara Anda

Microsoft Excel memungkinkan Anda melakukan lebih dari sekadar membuat spreadsheet — Anda juga dapat menggunakan perangkat lunak untuk menghitung fungsi utama, seperti hubungan antara dua variabel. Dikenal sebagai koefisien korelasi, metrik ini berguna untuk mengukur dampak dari satu operasi pada operasi lainnya untuk menginformasikan operasi bisnis.

Tidak percaya diri dengan keterampilan Excel Anda? Tidak masalah. Berikut cara menghitung — dan memahami — koefisien korelasi di Excel.

Koefisien korelasi +1 menunjukkan “korelasi positif sempurna”, yang berarti bahwa ketika variabel X meningkat, variabel Y meningkat pada tingkat yang sama. Sedangkan nilai korelasi -1 merupakan “korelasi negatif sempurna”, yang artinya semakin besar variabel X maka variabel Y semakin menurun dengan laju yang sama. Analisis korelasi juga dapat mengembalikan hasil di mana saja antara -1 dan +1, yang menunjukkan bahwa variabel berubah pada tingkat yang sama tetapi tidak identik.

Nilai korelasi dapat membantu bisnis mengevaluasi dampak tindakan tertentu pada tindakan lain. Misalnya, perusahaan mungkin menemukan bahwa ketika pengeluaran untuk pemasaran media sosial meningkat, begitu juga keterlibatan pelanggan, menunjukkan bahwa lebih banyak pengeluaran mungkin masuk akal.

Atau mereka mungkin menemukan bahwa kampanye iklan tertentu menghasilkan penurunan keterlibatan pelanggan yang berkorelasi, yang pada gilirannya menunjukkan perlunya evaluasi ulang upaya saat ini. Penemuan bahwa variabel tidak berkorelasi juga bisa berharga; sementara akal sehat mungkin menyarankan bahwa fungsi atau fitur baru dalam produk Anda akan berkorelasi dengan peningkatan keterlibatan, itu mungkin tidak memiliki dampak yang terukur. Analisis korelasi memungkinkan perusahaan untuk melihat hubungan ini (atau kekurangannya) dan membuat keputusan strategis yang baik.

Jadi bagaimana Anda menghitung koefisien koreksi di Excel? Sederhana! Ikuti langkah ini:

1. Buka Excel.

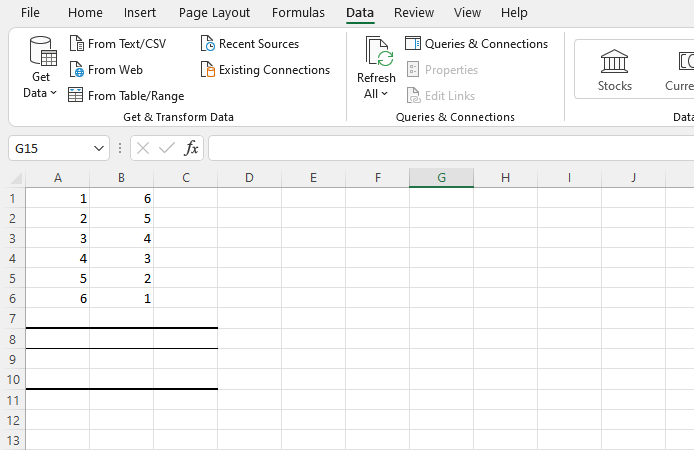
Langkah satu: Buka Excel dan mulai lembar kerja baru untuk data variabel terkait Anda. Masukkan titik data variabel pertama Anda di kolom A dan variabel kedua Anda di kolom B. Anda juga dapat menambahkan variabel tambahan di kolom C, D, E, dll. — Excel akan memberikan koefisien korelasi untuk masing-masing variabel.

Pada contoh di bawah, kita telah memasukkan enam baris data di kolom A dan enam baris di kolom B.

2. Instal Alat Analisis.

Selanjutnya? Jika Anda tidak memilikinya, instal Excel Analysis Toolpak.

Pilih "File", lalu "Options," dan Anda akan melihat layar ini:

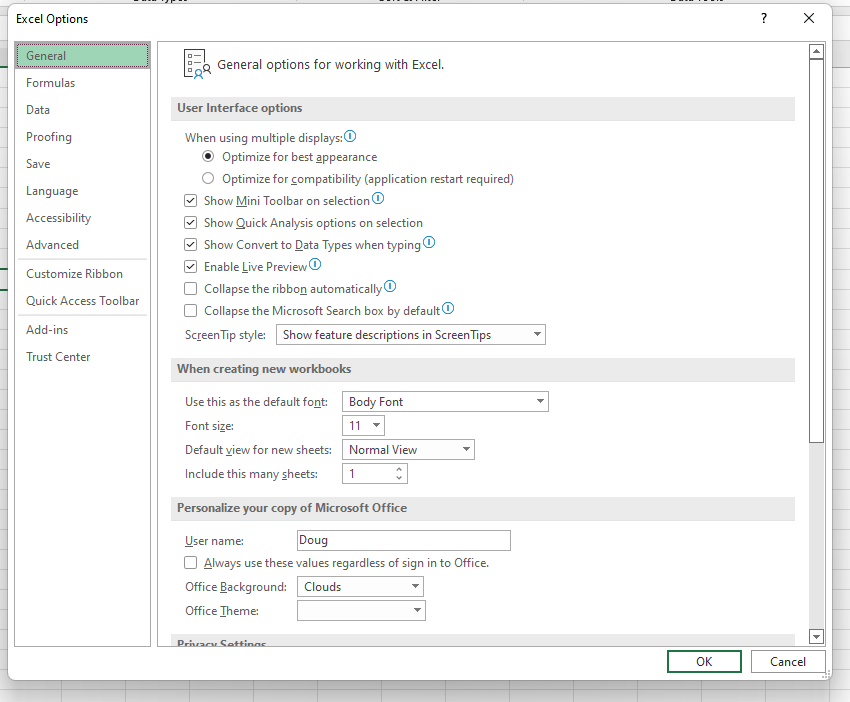
Pilih "Add-Ins" dan kemudian klik "Go".

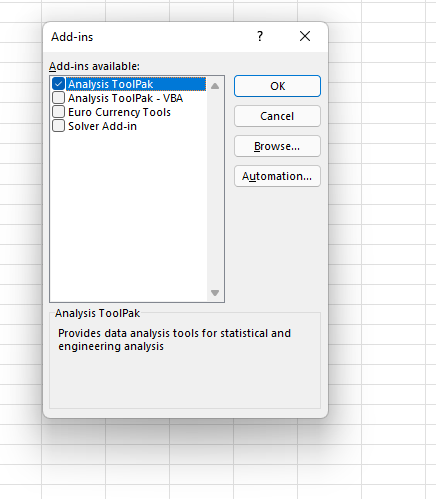
Sekarang, centang kotak yang bertuliskan "Analysis ToolPak" dan klik "Ok".

3. Pilih “Data” dari menu bar bagian atas.

Setelah Anda menginstal ToolPak, pilih "Data" dari menu bilah Excel atas. Ini memberi Anda submenu yang berisi berbagai opsi analisis untuk data Anda.

4. Pilih “Analisis Data” di sudut kanan atas.

Sekarang, cari "Analisis Data" di sudut kanan atas dan klik untuk mendapatkan layar ini:

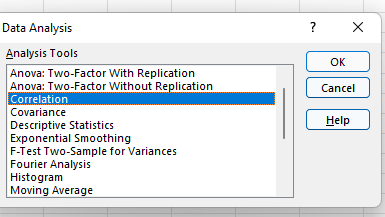
5. Pilih Korelasi.

Pilih Korelasi dari menu dan klik "OK."

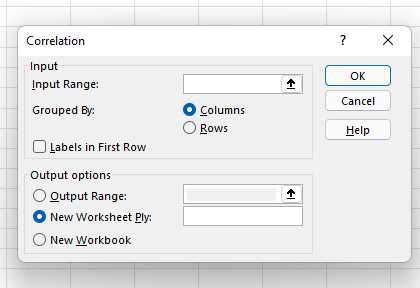
6. Tentukan jangkauan dan keluaran data Anda.

Sekarang tentukan rentang dan keluaran data Anda. Anda cukup mengklik kiri dan menyeret kursor Anda melintasi data yang ingin Anda pilih, dan itu akan terisi secara otomatis di kotak Korelasi. Terakhir, pilih rentang keluaran untuk data korelasi Anda — kami telah memilih A8. Kemudian, klik "Oke".

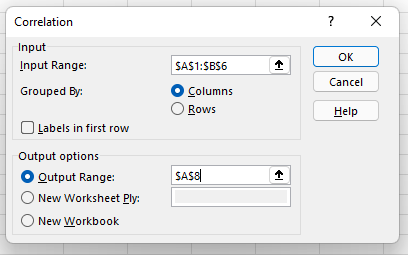
7. Evaluasi koefisien korelasi Anda.

Hasil korelasi Anda sekarang akan ditampilkan. Dalam contoh kita, nilai di kolom 1 dan kolom 2 memiliki korelasi negatif sempurna; ketika satu naik, yang lain turun dengan kecepatan yang sama.

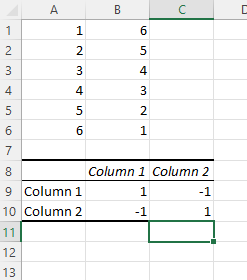
Matriks Korelasi Excel

Hasil korelasi Excel juga dikenal sebagai matriks korelasi Excel. Pada contoh di atas, dua kolom data kami menghasilkan matriks koreksi sempurna 1 dan -1. Tetapi apa yang terjadi jika kita menghasilkan matriks korelasi dengan kumpulan data yang kurang ideal?

Berikut data kami:

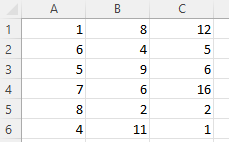
Dan inilah matriksnya:

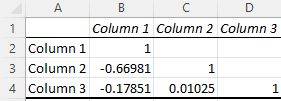
Sel C4 dalam matriks memberi kita korelasi antara Kolom 3 dan Kolom 2, yang sangat lemah 0,01025, sedangkan Kolom 1 dan Kolom 3 menghasilkan korelasi negatif yang lebih kuat sebesar -0,17851. Namun, sejauh ini korelasi terkuat adalah antara Kolom 1 dan Kolom 2 di -0,66891.

Jadi apa artinya ini dalam praktik? Katakanlah kita sedang memeriksa dampak tindakan tertentu pada kemanjuran kampanye media sosial, di mana Kolom 1 mewakili jumlah pengunjung yang mengklik iklan sosial dan Kolom 2 dan 3 mewakili dua tagline pemasaran yang berbeda. Matriks korelasi menunjukkan korelasi negatif yang kuat antara Kolom 1 dan 2, yang menunjukkan bahwa tagline versi Kolom 2 secara signifikan menurunkan keterlibatan pengguna secara keseluruhan, sedangkan Kolom 3 hanya mendorong sedikit penurunan.

Membuat matriks Excel secara teratur dapat membantu perusahaan lebih memahami dampak satu variabel terhadap variabel lain dan menentukan apa (jika ada) efek negatif atau positif yang mungkin ada.

Rumus Korelasi Excel

Jika Anda lebih suka memasukkan rumus korelasi sendiri, itu juga merupakan opsi. Berikut tampilannya:

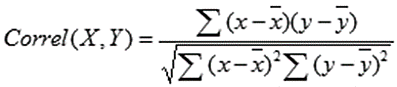
X dan Y adalah pengukuran Anda, adalah jumlah, dan X dan Y dengan batang di atasnya menunjukkan nilai rata-rata pengukuran. Anda akan menghitungnya sebagai berikut:

• Hitung jumlah variabel X dikurangi rata-rata X.
• Hitung jumlah variabel Y dikurangi rata-rata Y.
• Kalikan kedua hasil itu dan sisihkan angka itu (ini adalah hasil pertama).
• Kuadratkan jumlah X dikurangi rerata X. Kuadratkan jumlah Y dikurangi rerata Y. Kalikan kedua bilangan tersebut.
• Ambil akar kuadrat (ini adalah hasil kedua).
• Bagi hasil pertama dengan hasil kedua.
• Anda mendapatkan koefisien korelasi.

Mudah, kan? Iya dan tidak. Meskipun memasukkan angka tidak rumit, seringkali lebih banyak masalah daripada nilai untuk membuat dan mengelola formula ini. Toolpak Excel bawaan seringkali merupakan cara yang lebih sederhana (dan lebih cepat) untuk menunjukkan koefisien dan menemukan hubungan kunci.

Korelasi Bukan Sebab-Akibat

Tidak ada artikel tentang korelasi yang lengkap tanpa menyebutkan bahwa itu tidak sama dengan sebab-akibat. Dengan kata lain, hanya karena dua variabel naik atau turun bersama-sama tidak berarti bahwa satu variabel adalah penyebab kenaikan atau penurunan variabel lainnya.

Pertimbangkan beberapa contoh yang sangat aneh.

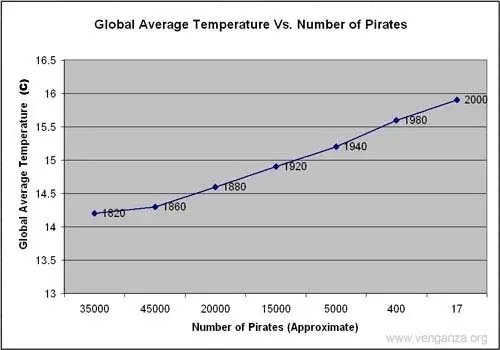
Gambar ini menunjukkan korelasi negatif yang hampir sempurna antara jumlah bajak laut dan suhu rata-rata global — karena bajak laut semakin langka, suhu rata-rata meningkat.

Masalah? Sementara kedua variabel ini berkorelasi, tidak ada hubungan sebab akibat antara keduanya; suhu yang lebih tinggi tidak mengurangi populasi bajak laut dan lebih sedikit bajak laut tidak menyebabkan pemanasan global.

Sementara korelasi adalah alat yang ampuh, itu hanya menunjukkan arah kenaikan atau penurunan antara dua variabel — bukan penyebab kenaikan atau penurunan ini. Untuk menemukan hubungan sebab akibat, perusahaan harus menambah atau mengurangi satu variabel dan mengamati dampaknya. Misalnya, jika korelasi menunjukkan bahwa keterlibatan pelanggan naik dengan pengeluaran media sosial, ada baiknya memilih sedikit peningkatan pengeluaran diikuti dengan pengukuran hasil. Jika lebih banyak pengeluaran mengarah langsung pada peningkatan keterlibatan, hubungan tersebut berkorelasi dan kausal. Jika tidak, mungkin ada satu (atau lebih) faktor yang mendukung peningkatan kedua variabel tersebut.

Mengikuti Korelasi

Korelasi Excel menawarkan titik awal yang kuat untuk pemasaran, penjualan, dan pengembangan strategi pembelanjaan, tetapi tidak menceritakan keseluruhan cerita. Akibatnya, ada baiknya menggunakan opsi analisis data bawaan Excel untuk mengevaluasi korelasi antara dua variabel dengan cepat dan menggunakan data ini sebagai titik awal untuk analisis yang lebih mendalam.