SVG 곡선 및 베지어 곡선: 계산 방법

SVG 곡선은 연속적인 부드러운 곡선입니다. 선, 곡선, 호 등을 만드는 데 사용할 수 있습니다. 가장 중요한 것은 베지어 곡선을 만드는 데 사용할 수 있다는 것입니다. 베지어 곡선은 4개의 점으로 정의되는 곡선입니다. 처음 두 점은 곡선의 시작점과 끝점이고 마지막 두 점은 제어점입니다. 제어점은 곡선의 모양을 결정합니다. 베지어 곡선을 계산하는 방법에는 여러 가지가 있습니다. 가장 일반적인 방법은 De Casteljau 알고리즘을 사용하는 것입니다. 이 알고리즘은 베지어 곡선의 점을 계산하는 데 사용됩니다. De Casteljau의 알고리즘은 재귀 알고리즘입니다. 즉, 문제를 더 작은 하위 문제로 나눕니다. 알고리즘은 베지어 곡선을 정의하는 네 개의 점에서 시작합니다. 그런 다음 시작점과 끝점 사이의 중간점을 계산합니다. 그런 다음 이 중간점을 사용하여 곡선의 다음 점을 계산합니다. 이 프로세스는 원하는 포인트 수에 도달할 때까지 반복됩니다. De Casteljau의 알고리즘이 베지어 곡선을 계산하는 유일한 방법은 아닙니다. B-스플라인 사용과 같은 다른 방법이 있습니다. 그러나 De Casteljau의 알고리즘은 가장 일반적인 방법이며 가장 자주 사용되는 방법입니다.

이것은 벡터 그래픽에 대한 이전 블로그 게시물에 대한 후속 조치입니다. SVG는 가볍고 빠르며 자연스럽기 때문에 조작 및 애니메이션을 쉽게 수행할 수 있습니다. 몇 가지 삽화의 도움을 받아 일련의 선과 곡선 주제로 돌아가겠습니다. 베지어 곡선은 원래 두 명의 프랑스 엔지니어의 이름을 따서 명명되었으며 공식적으로 채택되었습니다. 컨텍스트에 따라 절대 제어점 또는 상대 제어점으로 분류됩니다. 마우스 버튼이 눌리면 mouseDown 이벤트의 십자선이 나타나며, 점은 mouseDown 이벤트의 가로선과 세로선이 화면의 곡선과 교차하는 위치를 나타냅니다. 제어점은 이제 사용자 경험의 직관적인 부분이 된 Illustrator와 같은 벡터 그래픽 편집기에서 편집할 수 있습니다.

이 작업은 주로 utility/bezierIntersections.js에서 이루어집니다. 최대 3개의 세제곱 근이 있을 수 있으며 그 중 일부는 더 평평한 곡선 세그먼트에서 사양을 벗어난 근에 대한 정크 좌표일 수 있습니다. 곡선과 선의 교차점을 찾기 위해 곡선'/선' 정의를 사용합니다. 코드가 데모이기 때문에 정크 좌표를 정리하지 않았습니다. 대신 코드는 데모일 뿐이므로 대수학에 집중했습니다.

선을 따라 점 P를 찾으려면 공식 (1-t)P0 + (t)P1을 사용하십시오. P0은 시작점이고 P1은 끝점입니다.

베지어 곡선은 어떻게 계산됩니까?

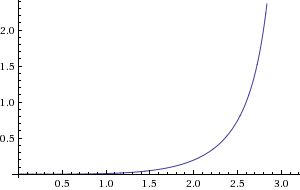
베지어 곡선은 곡선을 정의하기 위해 파라메트릭 방정식을 사용하여 계산됩니다. 파라메트릭 방정식은 곡선의 x 및 y 좌표를 매개변수 t의 함수로 정의합니다. 매개변수 t는 0과 1 사이의 실수일 수 있습니다. t가 0이면 곡선의 x 및 y 좌표는 첫 번째 제어점의 x 및 y 좌표입니다. t가 1이면 곡선의 x 및 y 좌표는 마지막 제어점의 x 및 y 좌표입니다. 0과 1 사이의 t 값의 경우 곡선의 x 및 y 좌표는 첫 번째 제어점과 마지막 제어점의 x 및 y 좌표 사이 어딘가에 있습니다.

컴퓨터 그래픽에서 자주 사용되는 기능은 경사 곡선을 사용하는 것입니다. 번스타인 다항식(t = (1 – t))*n = 1로 정의할 수 있습니다. 파이썬에서는 [0, 1] 범위의 곡선을 계산할 수 있습니다. 곡선의 모양은 0에서 1 사이에서 P1에 의해 완전히 결정되기 때문에 0에서 1이 될 수 있습니다. 행렬 곱셈을 사용하여 베지어 공식을 나타낼 수 있습니다. 각 다항식은 행렬의 계수가 모두 중앙에 있는 행렬의 두 Pi의 함수입니다. 이러한 방식으로 eq를 사용하여 제어점의 수에 관계없이 일반 곡선 버전을 프로그래밍할 수 있습니다. 일련의 점을 사용하여 부드러운 곡선을 그립니다.

(x0, y0), (x1, y1), (x2, y2), (x3, y3) 및 (x4, y4)의 제어점을 사용하여 접선 벡터를 그릴 때 접선 벡터의 각 점은 방향. 베지어 곡선은 포인트의 볼록 선체에 의해 형성됩니다. 정점이 (x0, y0), (x1, y1), (x2, y2) 및 (x3, y3)인 사변형은 4개의 점이 있는 구적 곡선의 결과입니다. 다음 방정식은 볼록 선체를 정의하는 데 사용됩니다. * x0)2의 제곱근은 * x0의 제곱근과 같습니다. (y) = b0)2. 베지어 곡선 방정식 의 경우 수행해야 할 작업은 다음과 같습니다. 다른 말로 하면 =. (x x0)2)와 같습니다. (02) Y=0)이 가장 적절한 조합입니다. B0,3은 (1*u)3의 단위입니다. 값 =. (x x0)2의 제곱근은 (x x0).2)의 제곱근과 같습니다. (Y0) 2는 이에 대한 공식입니다. (x x0)2)는 인접한 두 수의 합을 나타내는 값이다. y(y y0)의 경우 (y y0)을 사용해야 합니다. (x * x0)2)는 (x * x0)과 같습니다. = (x0 x1)2 + (y0 y1)2 = br>. 1,3=3u(1*u)2는 측정 단위입니다. B3,=3u2,(1*u)는 수학의 측정 ​​단위 유형입니다.

Svg 경로는 어떻게 작동합니까?

*경로는 선, 곡선, 호 및 기타 모양을 그릴 수 있습니다. 경로는 여러 개의 직선 또는 곡선으로 구성되어 복잡한 모양이 될 수 있습니다. 직선만으로 구성된 복잡한 도형을 s로 생성할 수 있습니다.

SVG 경로 의 단일 숫자나 문자는 위협적으로 보일 수 있습니다. 그러나 파일에는 많은 숫자와 문자가 있습니다. 이 단원에서는 경로를 사용하여 사각형을 그리고 그리기 도구를 사용하여 이 작업을 수행합니다. 변경 사항을 빠르게 확인할 수 있는 Codepen 또는 기타 도구는 코딩을 시작하기에 좋은 곳입니다. 우리의 최선의 노력에도 불구하고 우리는 그들을 위해 일을 더 쉽게 만들 수 있습니다. 결과적으로 직사각형의 오른쪽을 그릴 때 연필이 x축에 머무르고 y에서 200만큼 위로 이동하기를 원합니다. 위로 이동하기 위해 Y -200이 방정식에 추가됩니다. 그런 다음 z 명령을 사용하여 줄을 원래 위치로 되돌릴 수 있습니다.

Svg 경로 및 CSS

마이패스는 상징입니다. 높이:100px; width:115br> 너비 100px는 너비 *br과 같습니다.
svg path=”M10,L20″ *br Mypath %22br%22 이 이미지를 표시하려면 height:100px를 활성화하십시오. 이 너비를 표시하려면 *br>을 두 번 클릭하십시오. Mypath는 활성 디렉토리입니다.
배경: #FFF, *br*.

베지어 제어점은 어떻게 계산됩니까?

원하는 결과에 따라 베지어 제어점을 계산할 수 있는 다양한 방법이 있으므로 이 질문에 대한 확실한 답은 없습니다. 몇 가지 일반적인 방법에는 곡선의 끝점을 연결하는 선의 각도 이등분선을 사용하거나 곡선의 원하는 특성을 고려하는 방정식 시스템을 푸는 방법이 포함됩니다. 그러나 일반적으로 제어점은 일반적으로 지정된 끝점을 통과하는 부드러운 곡선을 생성하도록 선택됩니다.

프로그래밍에서 베지어 곡선은 잘 알려진 기능입니다. 그래픽에서 곡선의 확장 가능한 벡터 그래픽을 생성하는 데 사용되어 곡선을 통해 이동할 때 곡선이 부드럽게 유지되도록 합니다. 베지어 곡선을 그리려면 시작점, 끝점, 제어점 2개의 네 가지 점을 알아야 합니다. 시작점과 제어점 사이의 거리는 백분율 긴 경로를 기준으로 베지어 곡선을 계산하는 데 사용됩니다. 두 점의 중간점에 대해 M에 P0 및 P1을 곱합니다. 유투브 영상만큼은 거의 설명을 못드리니 더 알고싶으신 분들은 시청해주세요. 베지어 곡선을 따라 점 P의 값을 찾는 공식은 다음과 같습니다.

측정의 세 가지 기본 단위는 P0(점), P(선을 따른 점) 및 T(선을 따른 백분율)입니다. P1 = (알 수 없는 끝점)은 이 숫자를 찾는 공식입니다. 비율은 1 – p(t) – 0/p입니다.

시작점(중지점)에서 베지어 곡선에 접하는 벡터는 처음 두 개(마지막 두 개)를 연결하는 선에 수직입니다. 시작(중지) 지점에서 베지어 곡선에 접하는 벡터가 있지만 곡선이 오른쪽으로 기울어져 있습니다. 재귀 알고리즘으로 베지어 곡선을 수동으로 생성하는 것은 불가능합니다. 시스템은 첫 번째 제어점에서 시작하여 다음 제어점을 통과하는 곡선으로 끝납니다. 사용하기 간단하지만 모든 순서의 곡선을 만드는 데 사용할 수도 있습니다. 일반적으로 곡선은 첫 번째 제어점에서 시작됩니다. 두 번째 점에서 곡선은 y축과 교차합니다. 마지막으로 곡선은 세 번째 점에서 x축과 교차합니다. 네 번째 제어점은 곡선이 처음 두 제어점을 연결하는 선과 교차하는 지점에 있습니다. 다섯 번째 제어점은 곡선이 두 번째와 세 번째 제어점을 연결하는 선과 교차하는 지점에 있습니다. 여섯 번째 제어점은 커브가 선과 교차하는 지점이기 때문에 세 번째와 네 번째 제어점을 연결합니다. 일곱 번째 제어점은 곡선이 네 번째와 다섯 번째 제어점을 연결하는 선과 교차하는 지점입니다. 여덟 번째 제어점은 곡선이 다섯 번째와 여섯 번째 제어점을 연결하는 선과 교차하는 지점입니다. 아홉 번째 제어점은 커브가 여섯 번째와 일곱 번째 제어점을 연결하는 선과 교차하는 지점입니다. 곡선이 7번째와 8번째 제어점을 연결하는 선과 교차하면 10번째 제어점을 정의합니다. 제어점은 8번째와 9번째 제어점을 연결하는 선과 곡선이 교차하는 지점에서 각각 11번째와 9번째 제어점에 위치합니다. 12번째 제어점은 곡선이 9번째와 10번째 제어점을 연결하는 선과 교차하는 지점입니다. 곡선은 임의의 순서로 그릴 수 있지만 모든 점이 실제로 유용한 것은 아닙니다. 곡선의 시작과 끝에 있는 점이 일반적으로 가장 유용하지만 곡선의 중심에서도 유용할 수 있습니다. 베지어 곡선 알고리즘은 간단하지만 이를 사용하여 모든 모양을 만들 수 있습니다.

Svg에서 곡선을 어떻게 그리나요?

svg에서 곡선을 그리려면 요소를 만들고 여기에 광고 속성을 정의해야 합니다. d 속성은 요소의 경로 데이터를 정의합니다. 경로 데이터는 일련의 명령과 매개변수로 구성됩니다. 각 명령은 문자와 숫자로 구성됩니다. 문자는 명령을 나타내고 숫자는 매개변수를 나타냅니다. 곡선을 그리는 명령은 C, c, S, s, Q, q, T, t, A, a입니다. C 명령은 "절대 3차 베지어 곡선"을 나타냅니다. c 명령은 "상대 3차 베지어 곡선"을 나타냅니다. S 명령은 "absolute smooth cubic Bezier curve"를 나타냅니다. s 명령은 "상대적으로 부드러운 3차 베지어 곡선"을 나타냅니다. Q 명령은 "절대 2차 베지어 곡선"을 나타냅니다. q 명령은 "상대 2차 베지어 곡선"을 나타냅니다. T 명령은 "absolute smooth quadratic Bezier curve"를 나타냅니다. t 명령은 "상대적으로 부드러운 2차 베지어 곡선"을 나타냅니다. A 명령은 "절대 타원 호"를 나타냅니다. a 명령은 "상대 타원 호"를 나타냅니다. 이러한 각 명령에는 곡선을 정의하는 서로 다른 매개변수 세트가 있습니다.

3차 베지어 곡선 명령(C)은 다음과 같습니다: [code type=html]. =1, =1, =1, =1, =1, =1, =1, =1, =1, =1, =1, =1, =1, =1 곡선은 100,200점에서 시작하고, 경로가 진행되는 곳. 두 번째 기준점은 400,100입니다. 곡선의 끝 값은 400,200입니다. 곡선은 선과 마찬가지로 연속적으로 휘어질 필요가 없습니다. 하나의 곡선을 다른 곡선에 연결하면 훨씬 더 복잡한 곡선을 만들 수 있습니다. S 및 S라고도 하는 이러한 명령은 브라우저에서 원하는 것을 쉽게 찾을 수 있도록 하는 데 사용됩니다.

이번에는 절대 단축키를 사용하여 두 곡선을 표현합니다. 2차 베지어를 사용하려면 두 개가 아닌 하나의 제어점이 필요합니다. arc 명령을 사용하면 대부분의 매개변수가 고려됩니다. 곡선 명령에는 세 가지 유형이 있습니다. 시작점과 끝점, rx, ry 및 x축 회전이 있는 타원, 네 개의 호가 모두 가능합니다. 아크는 스윕 플래그 이미지에서 대형 아크 플래그 이미지를 미러링하는 데 사용됩니다. 파란색 호는 양쪽 끝이 같은 방향을 가리킬 때 축 주위에 형성되는 빨간색 호를 나타냅니다.

결과적으로 0 값은 더 작은 호를 사용해야 함을 나타내고 1 값은 더 큰 호를 사용해야 함을 나타냅니다. 경로는 기본 모양보다 더 크고 강력합니다. 조금 더 노력하면 만들 수 있지만 많지는 않습니다. 모든 그래픽 편집기가 이미지를 경로로 내보낼 가능성이 높습니다. 몇 분 안에 명령을 암기하는 것이 가장 좋습니다.

SVG에서 경로를 만드는 방법 알아보기

SVG에서 경로를 사용하면 원과 곡선을 비롯한 다양한 모양을 만들 수 있습니다. 이 기사에서는 이러한 명령을 사용하여 이러한 경로를 만드는 방법을 살펴보겠습니다.
A 명령은 SVG에서 호를 만드는 데 사용할 수 있습니다. 호 명령 창을 연 후 호를 생성하는 데 사용할 원 또는 타원의 x 및 y 반경을 지정할 수 있습니다. 호의 시작점과 끝점은 물론 호를 그려야 하는 각도도 포함할 수 있습니다.
C 명령을 사용하면 곡선 경로도 만들 수 있습니다. 사용하는 경우 그려야 하는 경로와 글리프 및 누락 글리프 요소를 지정합니다. 경로 정의는 각 명령이 해당 매개변수를 나타내는 명령 문자와 숫자로 표시되는 경로 명령 목록입니다.
예를 들어 SVG에서 경로를 중앙에 배치하려면 viewBox 속성을 사용할 수 있습니다. 문서에서 찾은 위치에 관계없이 뷰포트의 중앙에 경로를 배치합니다.

Svg 베지어 곡선 생성기

온라인에서 사용할 수 있는 여러 svg 베지어 곡선 생성기가 있습니다. 이 생성기를 사용하면 지정한 매개변수를 기반으로 사용자 정의 svg 베지어 곡선을 만들 수 있습니다. 너비, 높이, 제어점 수 및 곡선의 기타 측면을 제어할 수 있습니다. 이러한 생성기는 웹 프로젝트를 위한 사용자 지정 모양과 디자인을 만드는 좋은 방법이 될 수 있습니다.

SVG 경로 곡선

SVG 경로 곡선은 SVG 경로에 부드러운 곡선을 만드는 데 사용됩니다. 사용 가능한 곡선에는 2차 곡선, 3차 곡선, 호 곡선 및 부드러운 곡선의 네 가지 유형이 있습니다. 각 유형의 곡선에는 고유한 장점과 단점이 있으므로 당면한 작업에 적합한 유형의 곡선을 선택하는 것이 중요합니다. 2차 곡선은 가장 단순한 유형의 곡선이며 쉽게 만들고 조작할 수 있습니다. 입방 곡선은 더 복잡하며 더 자세한 모양을 만드는 데 사용할 수 있습니다. 호 곡선은 원형 또는 타원형 모양을 만드는 데 가장 적합합니다. 부드러운 곡선은 다른 세 가지 유형의 곡선을 조합한 것으로 다양한 모양을 만드는 데 사용할 수 있습니다.

경로는 객체의 모양을 한쪽, 선으로, 곡선으로(입방 및 2차 기울기 모두), 호 및 클로즈패스로 이동하여 정의되는 객체 윤곽의 형상입니다. 복합 경로(즉, 여러 하위 경로가 있는 경로)를 사용하여 개체에 도넛 구멍이 있을 수 있습니다. SVG 경로 의 구문, 동작 및 DOM 인터페이스와 표현 방법을 설명합니다. 경로 데이터 시퀀스의 각 명령은 단일 문자를 따릅니다. 경로 데이터의 구문은 간결하여 파일 크기를 최소화하는 동시에 효율적인 다운로드를 가능하게 합니다. 경로 데이터의 문자에는 개행 문자가 포함되어 있으므로 가독성을 높이기 위해 경로 데이터를 여러 줄로 나눌 수 있습니다. 마크업에서 정규화된 공백 문자를 활용하면 속성 이름의 새 줄이 정규화됩니다.

이 값은 경로 데이터 문자열이 지정하는 모양을 나타냅니다. 문자열 내의 오류는 경로 데이터의 경로 데이터 오류 처리 섹션에 따라 처리됩니다. 경로 데이터 세그먼트(있는 경우)는 moveto 명령(있는 경우)으로 시작해야 합니다. 직선은 현재 지점에서 현재 하위 경로의 시작 지점까지 자동으로 그려집니다. 이 경로 세그먼트에는 길이가 없을 수 있습니다. 클로즈패스는 마지막 세그먼트의 끝에서 'stroke-linejoin' 값을 사용하여 초기 세그먼트의 시작으로 연결되는 경로로 정의됩니다. 첫 번째와 마지막 경로 세그먼트가 결합되지 않은 경우 닫힌 하위 경로와 열린 하위 경로 간에 차이가 있습니다.

Python은 현재 세그먼트 완료 경로 닫기 작업을 명령으로 지원하지 않습니다. 기준점을 변경하기 위해 명령 라인은 한 지점에서 다음 지점으로 직선을 그릴 수 있습니다. 상대 l 명령을 사용하여 라인을 생성할 때 끝점은 (cpy x)입니다. 양의 x축 방향으로 수평선을 그리려면 양의 x 값과 함께 상대 h 명령을 사용합니다. 처음 다섯 개의 예는 베지어 경로 의 단일 입방체 세그먼트를 보여줍니다. 내림차순으로 타원형 호를 명령할 수 있습니다. 상대 명령을 사용하는 경우 호는 좌표(cxy)로 표시됩니다.

큰 플래그와 스윕 플래그는 아래 다이어그램과 같이 그려진 호의 수를 나타냅니다. EBNF 처리는 캐릭터가 해당 생산에 대한 요구 사항을 더 이상 충족하지 않는 지점에서 중지하기 위해 가능한 한 주어진 생산을 많이 소비해야 합니다. d 속성 값이 0이면 렌더링이 비활성화됩니다. 캡 모양을 계산하고 세그먼트 경계에 마커를 표시할 때 세그먼트 경계에 대해 재정의가 활성화됩니다. rx와 ry가 모두 0이면 이 호는 직선 세그먼트(끝점을 연결하는 선)로 간주됩니다. 이 스케일링 작업에 대한 자세한 내용은 수학 공식에 대한 부록 섹션을 참조하십시오. 길이가 0인 경로 세그먼트는 유효하지 않으며 다음과 같은 경우 렌더링에 영향을 미칩니다.

경로에 'pathLength' 속성을 추가함으로써 작성자는 사용자 에이전트가 경로를 따라 거리를 계산할 수 있도록 경로의 총 길이를 계산할 수 있습니다. '경로' 요소 내에서 이동 작업은 길이가 0인 작업으로 간주될 수 있습니다. 몇 개의 선, 곡선 및 화살표만 경로 길이를 계산하는 데 사용할 수 있습니다.

경로, 곡선 및 호: 경로 요소의 기본 사항

경로는 일반적으로 '선' 요소를 사용하여 정의되며 이를 사용하여 직선을 만들 수 있습니다. 또한 'curve' 요소를 사용하여 'fill' 또는 'stroke' 요소로 곡선을 채울 수 있습니다.
몇 개의 다른 지점을 통과하는 경로를 만들고 싶다면 'arc' 요소를 사용할 수 있습니다. 'arc' 요소는 시작점과 끝점이라는 두 가지 특성을 가지고 있습니다. 반지름을 지정하여 호의 크기를 지정할 수도 있습니다.
마지막으로 모양을 사용하여 경로를 만들 수 있습니다. '경로' 요소에는 시작점과 끝점이라는 두 가지 요소가 있습니다. 광고 요소라고도 하는 학위 속성은 경로 요소의 일부로 포함됩니다. 도형 주위의 경로 이동 정도는 여기에서 지정됩니다.
결과적으로 경로를 사용하는 방법은 무수히 많으며 그 구성 요소는 모두 '경로' 요소에 요약되어 있습니다. 경로 요소에는 단일 속성이 포함되어 있으므로 그릴 모양을 알려주는 'd' 속성은 단일 속성을 포함하고 있음을 기억해야 합니다.

SVG 경로 예

SVG 경로는 개체의 모양을 일련의 연결된 선과 곡선으로 정의합니다. svg 경로 예제는 하트 모양을 정의합니다.

경로 요소는 도면의 마지막 요소입니다. 무엇을 그리는지 설명하려면 d 속성이 필요합니다. 여기에는 많은 기능이 있지만 대부분은 쉽게 식별할 수 있고 해독할 수 없는 값을 가진 미니 구문에 불과합니다. 이해하기 쉽도록 코드를 다시 포맷할 수 있습니다(여전히 원래 문자가 있음). 경로를 사용하여 펜을 설정한 지점으로 다시 직선을 그릴 수 있으므로 저렴하고 간단한 방법입니다. 경로는 다른 명령과 마찬가지로 Z(또는 z, 상관 없음)로 닫혀야 하며 선택적 명령입니다. 지금까지 A 명령이 가장 어렵습니다. 타원의 너비, 높이 및 회전을 결정하려면 예상되는 경로를 지정합니다. 이동 경로에는 두 개의 가능한 타원이 있습니다. 각 타원에는 두 개의 다른 경로가 있고 각 타원에는 네 개의 다른 경로가 있습니다.

큐빅 베지어

3차 베지어 곡선은 컴퓨터 그래픽 및 관련 분야에서 자주 사용되는 파라메트릭 곡선입니다. 곡선은 4개의 점, 즉 2개의 끝점과 2개의 제어점으로 정의됩니다. 베지어 곡선을 결합하여 끝과 끝이 결합된 여러 베지어 곡선으로 구성된 부분적으로 정의된 곡선인 베지어 스플라인을 형성할 수 있습니다.

이 비디오에서 베지어 곡선 이면의 수학 및 다른 타이밍 기능과의 관계를 이해하십시오. 대화형 시각화를 사용하여 이러한 아름다운 전환 이면의 수학을 반영하도록 시각화를 사용자 지정할 수 있습니다. 곡선은 한 상태에서 다음 상태로 이동하는 과정을 묘사하는 데 사용할 수 있는 특수 유형의 곡선입니다. 이제 축 P0 -> P1 및 P1 -> P2의 세그먼트 간에 연속적으로 이동할 수 있습니다. 이 두 점을 세그먼트와 연결하고 그 위에 보간된 점(파란색 점)을 배치하면 2차 베지어 곡선과 유사한 경로를 얻을 수 있습니다. 이것은 선형 보간으로 알려져 있습니다. 제어점 P0, P1, P2 및 P3부터 시작하여 수식을 사용하여 큐브-베지어 곡선을 나타냅니다.

4개의 점을 연결하는 각 세그먼트에 네 번째 점인 P4를 추가하면 세그먼트 사이에 보간된 점을 얻습니다. 결과적으로 이러한 점을 연결하고 각각의 새 세그먼트(녹색)에 대해 (*)보간된(*) 점을 만듭니다. 다음 단계는 점을 연결하고 각 점의 세그먼트를 그리는 것입니다. 마지막으로 곡선을 그리는 공식이 있습니다. 다음은 cubebezier 공식을 표현하는 몇 가지 방법입니다. ( P0, P1, P2, P3) = for (let = 0, t = 1 <= 1); t = 1 즉, 방정식은 60에 대해 1을 갖습니다. res.

푸시( x: valX, y: valY ); 해상도 좌표 P1과 P2는 요소의 동작을 나타내며 전환할 때 이 곡선을 따릅니다. 이것이 수학적 개념이 운동으로 변환되는 방식입니다. 특정 cubebezier 전환과 함께 특정 곡선을 사용하여 다양한 부드럽게 전환을 나타낼 수 있습니다. 편의상 이러한 모든 타이밍 기능은 CSS에서 제공합니다. Framer Motion은 전환 개체의 easing 및 imigrate 함수 간에 강한 관계가 있음을 발견했습니다. Framing Motion의 cubic- bezier 기능은 CSS에서 본 것과 크게 다릅니다.

이 전환을 설명하려면 P1 및 P2 포인트 값을 각각 ease 속성에 전달해야 합니다. 이 블로그 게시물은 우리가 일상적으로 사용하는 몇 가지 멋진 기능에 대한 몇 가지 흥미로운 통찰력을 제공했으며 귀하의 관심을 끌었기를 바랍니다. cubic- bezier 기능 과 지침에 대한 더 많은 지식이 있으면 새로운 전환과 애니메이션을 쉽게 만들 수 있습니다.