Obliczanie korelacji w programie Excel: Twój poradnik

Program Microsoft Excel umożliwia nie tylko tworzenie arkuszy kalkulacyjnych — można również używać oprogramowania do obliczania kluczowych funkcji, takich jak relacje między dwiema zmiennymi. Ta metryka, znana jako współczynnik korelacji, jest przydatna do mierzenia wpływu jednej operacji na inną w celu informowania operacji biznesowych.

Nie masz pewności co do swoich umiejętności obsługi Excela? Nie ma problemu. Oto jak obliczyć — i zrozumieć — współczynnik korelacji w programie Excel.

Współczynnik korelacji +1 wskazuje na „idealną korelację dodatnią”, co oznacza, że ​​wraz ze wzrostem zmiennej X, zmienna Y rośnie w tym samym tempie. Tymczasem wartość korelacji -1 jest „idealną korelacją ujemną”, co oznacza, że ​​gdy zmienna X rośnie, zmienna Y maleje w tym samym tempie. Analiza korelacji może również zwracać wyniki w zakresie od -1 do +1, co wskazuje, że zmienne zmieniają się w podobnym, ale nie identycznym tempie.

Wartości korelacji mogą pomóc firmom ocenić wpływ określonych działań na inne działania. Na przykład firmy mogą stwierdzić, że wraz ze wzrostem wydatków na marketing w mediach społecznościowych rośnie zaangażowanie klientów, co wskazuje, że większe wydatki mogą mieć sens.

Mogą też stwierdzić, że określone kampanie reklamowe powodują skorelowany spadek zaangażowania klientów, co z kolei sugeruje potrzebę ponownej oceny dotychczasowych wysiłków. Odkrycie, że zmienne nie są ze sobą skorelowane, również może być cenne; chociaż zdrowy rozsądek może sugerować, że nowa funkcja lub funkcja w Twoim produkcie będzie korelować ze zwiększonym zaangażowaniem, może nie mieć wymiernego wpływu. Analiza korelacji pozwala firmom zobaczyć tę relację (lub jej brak) i podejmować rozsądne decyzje strategiczne.

Jak więc obliczyć współczynnik korekcji w programie Excel? Prosty! Wykonaj następujące kroki:

1. Otwórz Excela.

Krok pierwszy: Otwórz program Excel i rozpocznij nowy arkusz dla skorelowanych danych zmiennych. Wprowadź punkty danych pierwszej zmiennej w kolumnie A i drugiej zmiennej w kolumnie B. Możesz również dodać dodatkowe zmienne w kolumnach C, D, E itd. — Excel zapewni współczynnik korelacji dla każdej z nich.

W poniższym przykładzie wprowadziliśmy sześć wierszy danych w kolumnie A i sześć w kolumnie B.

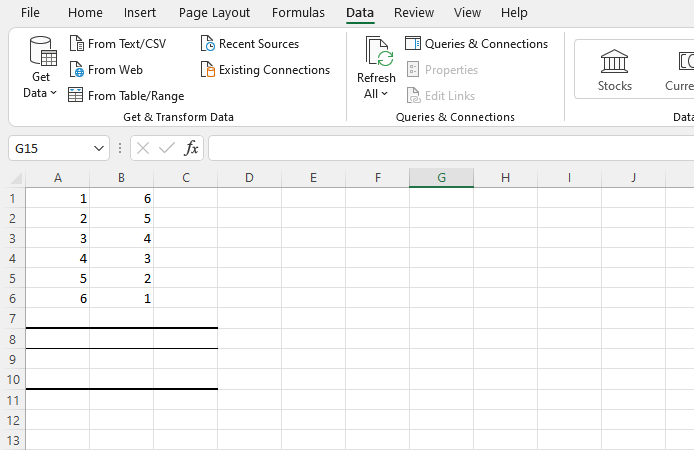
2. Zainstaluj pakiet narzędzi analitycznych.

Dalej? Jeśli go nie masz, zainstaluj pakiet narzędzi analizy programu Excel.

Wybierz „Plik”, a następnie „Opcje”, a zobaczysz ten ekran:

Wybierz „Dodatki”, a następnie kliknij „Idź”.

Teraz zaznacz pole „Analysis ToolPak” i kliknij „OK”.

3. Wybierz „Dane” z górnego paska menu.

Po zainstalowaniu pakietu ToolPak wybierz „Dane” z górnego menu paska Excel. Zapewnia to podmenu zawierające różne opcje analizy danych.

4. Wybierz „Analiza danych” w prawym górnym rogu.

Teraz poszukaj „Analiza danych” w prawym górnym rogu i kliknij ją, aby wyświetlić ten ekran:

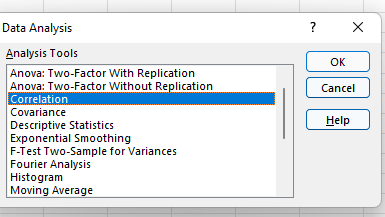
5. Wybierz Korelacja.

Wybierz Korelacja z menu i kliknij "OK".

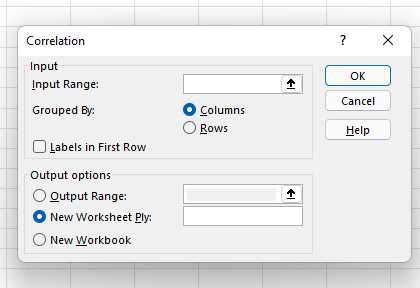
6. Zdefiniuj zakres danych i dane wyjściowe.

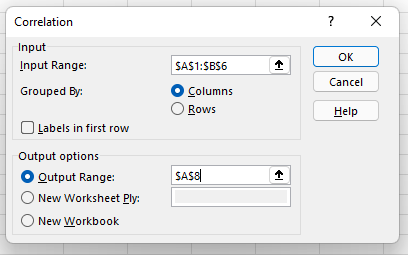
Teraz zdefiniuj zakres danych i dane wyjściowe. Możesz po prostu kliknąć lewym przyciskiem myszy i przeciągnąć kursor po danych, które chcesz wybrać, a zostaną one automatycznie wypełnione w polu Korelacja. Na koniec wybierz zakres wyjściowy dla swoich danych korelacji — wybraliśmy A8. Następnie kliknij „OK”.

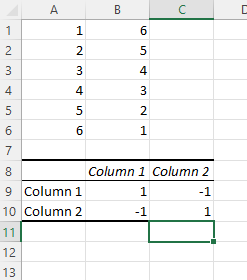
7. Oceń swój współczynnik korelacji.

Twoje wyniki korelacji zostaną teraz wyświetlone. W naszym przykładzie wartości w kolumnie 1 i kolumnie 2 mają doskonałą korelację ujemną; gdy jeden idzie w górę, drugi spada w tym samym tempie.

Macierz korelacji programu Excel

Wyniki korelacji programu Excel są również znane jako macierz korelacji programu Excel. W powyższym przykładzie nasze dwie kolumny danych dały idealną macierz korekcji 1 i -1. Ale co się stanie, jeśli stworzymy macierz korelacji z mniej idealnym zestawem danych?

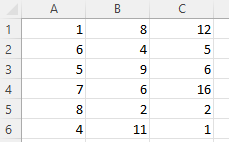
Oto nasze dane:

A oto macierz:

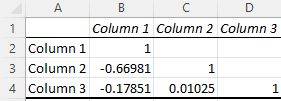
Komórka C4 w macierzy daje nam korelację między kolumną 3 a kolumną 2, która jest bardzo słaba 0,01025, podczas gdy kolumna 1 i kolumna 3 dają silniejszą korelację ujemną -0,17851. Jednak zdecydowanie najsilniejsza korelacja występuje między kolumną 1 a kolumną 2 przy -0,66891.

Więc co to oznacza w praktyce? Załóżmy, że badaliśmy wpływ określonych działań na skuteczność kampanii w mediach społecznościowych, gdzie kolumna 1 reprezentuje liczbę odwiedzających, którzy klikają reklamy społecznościowe, a kolumny 2 i 3 reprezentują dwa różne slogany marketingowe. Macierz korelacji pokazuje silną ujemną korelację między kolumnami 1 i 2, co sugeruje, że wersja sloganu z kolumny 2 znacznie zmniejszyła ogólne zaangażowanie użytkowników, podczas gdy kolumna 3 spowodowała tylko niewielki spadek.

Regularne tworzenie macierzy Excela może pomóc firmom lepiej zrozumieć wpływ jednej zmiennej na drugą i określić, jakie (jeśli w ogóle) mogą wystąpić negatywne lub pozytywne skutki.

Wzór korelacji Excel

Jeśli wolisz samodzielnie wprowadzić wzór korelacji, jest to również opcja. Oto jak to wygląda:

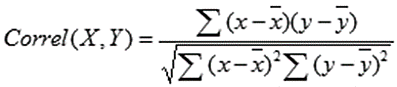
X i Y to twoje pomiary, ∑ to suma, a X i Y z paskami nad nimi wskazują średnią wartość pomiarów. Można to obliczyć w następujący sposób:

• Oblicz sumę zmiennej X minus średnia X.
• Oblicz sumę zmiennej Y minus średnia Y.
• Pomnóż te dwa wyniki i odłóż tę liczbę na bok (to jest pierwszy wynik).
• Podnieś do kwadratu sumę X minus średnia X. Podnieś do kwadratu sumę Y minus średnia Y. Pomnóż te dwie liczby.
• Wyciągnij pierwiastek kwadratowy (to jest drugi wynik).
• Podziel pierwszy wynik przez drugi wynik.
• Otrzymujesz współczynnik korelacji.

Łatwe, prawda? Tak i nie. O ile wstawianie liczb nie jest skomplikowane, to często więcej kłopotów niż tworzenie i zarządzanie tą formułą. Wbudowany pakiet narzędzi Excel Toolpak jest często prostszym (i szybszym) sposobem określania współczynników i odkrywania kluczowych relacji.

Korelacja ≠ Nie przyczynowość

Żaden artykuł o korelacji nie jest kompletny bez wzmianki, że nie jest to równoznaczne z przyczynowością. Innymi słowy, tylko dlatego, że dwie zmienne rosną lub spadają razem, nie oznacza, że ​​jedna zmienna jest przyczyną wzrostu lub spadku drugiej zmiennej.

Rozważ kilka bardzo dziwnych przykładów.

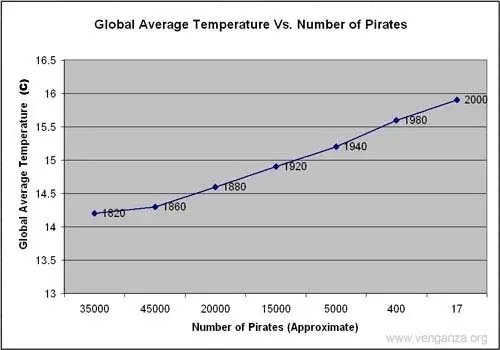
Ten obraz pokazuje prawie idealną ujemną korelację między liczbą piratów a średnią temperaturą na świecie — gdy piratów było coraz mniej, średnia temperatura wzrastała.

Problem? Chociaż te dwie zmienne są skorelowane, nie ma między nimi związku przyczynowego; wyższe temperatury nie zmniejszyły populacji piratów, a mniej piratów nie spowodowało globalnego ocieplenia.

Chociaż korelacja jest potężnym narzędziem, wskazuje jedynie kierunek wzrostu lub spadku między dwiema zmiennymi — a nie przyczynę tego wzrostu lub spadku. Aby odkryć powiązania przyczynowe, firmy muszą zwiększyć lub zmniejszyć jedną zmienną i obserwować wpływ. Na przykład, jeśli korelacja pokazuje, że zaangażowanie klientów rośnie wraz z wydatkami na media społecznościowe, warto zdecydować się na niewielki wzrost wydatków, a następnie pomiar wyników. Jeśli większe wydatki prowadzą bezpośrednio do większego zaangażowania, związek jest zarówno skorelowany, jak i przyczynowy. Jeśli nie, może istnieć jeden (lub więcej) czynnik, który leży u podstaw wzrostu obu zmiennych.

Nadążanie za korelacjami

Korelacje w programie Excel stanowią solidny punkt wyjścia do opracowywania strategii marketingu, sprzedaży i wydatków, ale nie opowiadają całej historii. W rezultacie warto skorzystać z wbudowanych opcji analizy danych programu Excel, aby szybko ocenić korelację między dwiema zmiennymi i wykorzystać te dane jako punkt wyjścia do bardziej dogłębnej analizy.