Krzywe SVG i krzywe Beziera: jak je obliczyć

Krzywa SVG to ciągła gładka krzywa. Można go używać do tworzenia linii, krzywych, łuków i nie tylko. Co najważniejsze, można go używać do tworzenia krzywych Beziera . Krzywa Beziera to krzywa zdefiniowana przez cztery punkty. Pierwsze dwa punkty to punkty początkowe i końcowe krzywej, a dwa ostatnie to punkty kontrolne. Punkty kontrolne określają kształt krzywej. Istnieje wiele sposobów obliczania krzywej Beziera. Najpopularniejszym sposobem jest użycie algorytmu De Casteljau. Algorytm ten służy do obliczania punktów na krzywej Beziera. Algorytm De Casteljau jest algorytmem rekurencyjnym. Oznacza to, że rozkłada problem na mniejsze podproblemy. Algorytm zaczyna się od czterech punktów definiujących krzywą Beziera. Następnie oblicza punkt środkowy między punktem początkowym i końcowym. Ten punkt środkowy jest następnie używany do obliczenia następnego punktu na krzywej. Proces ten jest powtarzany aż do osiągnięcia żądanej liczby punktów. Algorytm De Casteljau nie jest jedynym sposobem obliczania krzywej Beziera. Istnieją inne metody, takie jak użycie B-splajnów. Jednak algorytm De Casteljau jest najpowszechniejszą metodą i jest najczęściej używany.

Jest to kontynuacja mojego poprzedniego wpisu na blogu o grafice wektorowej. Manipulacja i animacja są łatwe do wykonania za pomocą plików SVG, ponieważ są lekkie, szybkie i naturalne. Powrócimy do tematu sekwencji linii i krzywych za pomocą kilku ilustracji. krzywe Beziera zostały pierwotnie nazwane na cześć dwóch francuskich inżynierów i zostały przez nich formalnie zaadaptowane. Są one klasyfikowane jako bezwzględne lub względne punkty kontrolne w zależności od kontekstu. Po naciśnięciu przycisku myszy pojawiają się krzyżyki zdarzenia mouseDown, a punkty wskazują, gdzie linie poziome i pionowe zdarzenia mouseDown przecinają się z krzywą na ekranie. Punkty kontrolne można teraz edytować w edytorach grafiki wektorowej, takich jak Illustrator, co stało się intuicyjną częścią doświadczenia użytkownika.

Ta akcja ma miejsce głównie w pliku tools/bezierIntersections.js. Mogą istnieć aż trzy pierwiastki sześcienne, a niektóre z nich mogą być śmieciowymi współrzędnymi pierwiastków spoza specyfikacji na bardziej płaskich segmentach krzywej. Aby znaleźć punkt przecięcia krzywych i prostych, używamy definicji krzywych/linii. Ponieważ kod jest demo, nie czyściłem współrzędnych śmieci; zamiast tego skoncentrowałem się na algebrze, ponieważ kod jest tylko demo.

Użyj wzoru (1-t)P0 + (t)P1, jeśli chcesz znaleźć dowolny punkt P wzdłuż prostej: P0 jest punktem początkowym, a P1 jest punktem końcowym.

Jak obliczane są krzywe Beziera?

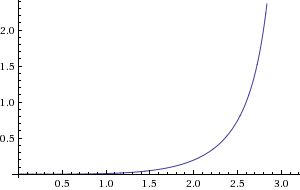
Krzywe Beziera są obliczane przy użyciu równania parametrycznego w celu zdefiniowania krzywej. Równanie parametryczne definiuje współrzędne x i y krzywej jako funkcję parametru t. Parametr t może być dowolną liczbą rzeczywistą z przedziału od 0 do 1. Gdy t wynosi 0, współrzędne x i y krzywej są współrzędnymi x i y pierwszego punktu kontrolnego. Gdy t wynosi 1, współrzędne x i y krzywej są współrzędnymi x i y ostatniego punktu kontrolnego. Dla wartości t między 0 a 1 współrzędne x i y krzywej leżą gdzieś pomiędzy współrzędnymi x i y pierwszego i ostatniego punktu kontrolnego.

Często używaną funkcją w grafice komputerowej jest stosowanie krzywych ukośnych. Można je zdefiniować za pomocą wielomianów Bernsteina (t = (1 – t))*n = 1. W Pythonie możemy obliczyć krzywą zakresu [0, 1]. Ponieważ kształt krzywej jest całkowicie określony przez P1 w zakresie od 0 do 1, może wynosić od 0 do 1. Do przedstawienia wzoru Beziera można użyć mnożenia macierzy. Każdy wielomian jest funkcją dwóch Pis w macierzy, ze wszystkimi współczynnikami macierzy wyśrodkowanymi na nich. W ten sposób możemy zaprogramować ogólną wersję krzywej dla dowolnej liczby punktów kontrolnych za pomocą równania. Narysuj gładką krzywą za pomocą zestawu punktów.

Gdy wektor styczny jest rysowany z punktami kontrolnymi w punktach (x0, y0), (x1, y1), (x2, y2), (x3, y3) i (x4, y4), każdy punkt wektora stycznego ma ten sam kierunek. Krzywa Beziera jest utworzona przez wypukłą otoczkę punktów. Czworokąt o wierzchołkach w punktach (x0, y0), (x1, y1), (x2, y2) i (x3, y3) jest wynikiem krzywej kwadraturowej z czterema punktami. Następujące równania są używane do zdefiniowania wypukłej otoczki. Pierwiastek kwadratowy z * x0)2 jest równy pierwiastkowi kwadratowemu z * x0. (y) = b0)2. Oto, co powinieneś zrobić w przypadku równania krzywej Beziera . Ujmując to inaczej, =. Jest równe (x x0)2). (02) Y=0) jest najbardziej odpowiednią kombinacją. B0,3 jest jednostką (1*u)3. Wartość =. Pierwiastek kwadratowy z (x x0)2 równa się pierwiastek kwadratowy z (x x0).2). (Y0) 2 to wzór na to. (x x0)2) to wartość oznaczająca sumę dwóch sąsiednich liczb. Jeśli chodzi o y (y y0), musimy użyć (y y0). Dla (x * x0)2) jest równe (x * x0). = (x0 x1)2 + (y0 y1)2 = br>. 1,3=3u(1*u)2 to jednostka miary. B3,=3u2,(1*u) to rodzaj jednostki miary w matematyce.

Jak działa ścieżka Svg?

The *ścieżka Jest w stanie rysować linie, krzywe, łuki i inne kształty. Ścieżka może składać się z wielu linii prostych lub krzywych, co daje złożone kształty. Złożone kształty złożone tylko z linii prostych można generować jako s.

Pojedyncza liczba lub litera w ścieżce SVG może wydawać się onieśmielająca; jednak w plikach jest dużo cyfr i liter. W tej lekcji użyjemy ścieżki do narysowania prostokąta i użyjemy do tego narzędzia do rysowania. Codepen lub inne narzędzie, które pozwala szybko zobaczyć, jakie zmiany są wprowadzane, jest dobrym miejscem do rozpoczęcia kodowania. Mimo naszych najlepszych starań możemy im ułatwić życie. W rezultacie, rysując naszą prawą stronę naszego prostokąta, chcemy, aby nasz ołówek pozostał na osi x, podczas gdy przesuwa się w górę o 200 na osi y. Y -200 jest dodawane do równania w celu przesunięcia w górę. Następnie możemy użyć polecenia z, aby przywrócić linię do pierwotnej pozycji.

Ścieżki Svg i CSS

Mypath jest symbolem. Wysokość: 100 pikseli; width:115br> Szerokość 100px równa się szerokości *br.
svg path=”M10,L20″ *br Mypath %22br%22 Aby wyświetlić ten obraz, włącz height:100px. Kliknij dwukrotnie *br>, aby wyświetlić tę szerokość. Mypath to aktywny katalog.
Tło: #FFF, *br*.

Jak obliczane są punkty kontrolne Beziera?

Nie ma jednej ostatecznej odpowiedzi na to pytanie, ponieważ istnieje wiele sposobów obliczania punktów kontrolnych Beziera w zależności od pożądanego wyniku. Niektóre popularne metody obejmują wykorzystanie dwusiecznych kątów linii łączących punkty końcowe krzywej lub rozwiązanie układu równań uwzględniających pożądane właściwości krzywej. Na ogół jednak punkty kontrolne są zazwyczaj wybierane w taki sposób, aby tworzyły gładką krzywą przechodzącą przez dane punkty końcowe.

W programowaniu krzywe Beziera są dobrze znaną funkcją. Są one używane w grafice do tworzenia skalowalnych grafik wektorowych krzywych, zapewniając, że krzywa pozostaje gładka podczas przesuwania się po krzywej. Aby narysować krzywą Beziera, musisz znać cztery punkty: punkt początkowy, punkt końcowy i dwa punkty kontrolne. Odległość między punktem początkowym a punktami kontrolnymi, oparta na procentowej długości ścieżki, jest używana do obliczenia krzywej Beziera. Dla punktu środkowego dwóch punktów pomnóż M przez P0 i P1. Nie potrafię tego wyjaśnić tak dobrze, jak w filmie na YouTube, więc obejrzyj go, jeśli chcesz dowiedzieć się więcej. Wzór na znalezienie wartości punktu P wzdłuż krzywej Beziera podano poniżej.

Trzy podstawowe jednostki miary to P0 (punkt), P (punkt wzdłuż linii) i T (procent wzdłuż linii). P1 = (nieznany punkt końcowy) to wzór na znalezienie tej liczby. Stosunek wynosi 1 – p (t) – 0 / p.

Wektor styczny do krzywej Beziera na początku (stopie) jest prostopadły do ​​linii łączącej dwa pierwsze (dwa ostatnie). Na początku (stopie) jest wektor styczny do krzywej Beziera, ale krzywa jest nachylona w prawo. Niemożliwe jest ręczne wygenerowanie krzywej Beziera za pomocą algorytmu rekurencyjnego. System rozpoczyna się od pierwszego punktu kontrolnego i kończy krzywą przechodzącą przez następny punkt kontrolny. Jest prosty w użyciu, ale może być również używany do tworzenia krzywych dowolnej kolejności. Ogólnie krzywa zaczyna się w pierwszym punkcie kontrolnym. W drugim punkcie krzywa przecina oś y. Wreszcie krzywa przecina oś x w trzecim punkcie. Czwarty punkt kontrolny znajduje się w punkcie, w którym krzywa przecina linię łączącą dwa pierwsze punkty kontrolne. Piąty punkt kontrolny znajduje się w punkcie, w którym krzywa przecina się z linią łączącą drugi i trzeci punkt kontrolny. Szósty punkt kontrolny łączy trzeci i czwarty punkt kontrolny, ponieważ jest to punkt, w którym krzywa przecina linię. Siódmy punkt kontrolny to punkt, w którym krzywa przecina linię łączącą czwarty i piąty punkt kontrolny. Ósmy punkt kontrolny to punkt, w którym krzywa przecina się z linią łączącą piąty i szósty punkt kontrolny. Dziewiąty punkt kontrolny to punkt, w którym krzywa przecina linię łączącą szósty i siódmy punkt kontrolny. Kiedy krzywa przecina linię łączącą siódmy i ósmy punkt kontrolny, definiowane są punkty dziesiątego punktu kontrolnego. Punkty kontrolne znajdują się odpowiednio na jedenastym i dziewiątym punkcie kontrolnym, w punkcie, w którym krzywa przecina się z linią łączącą ósmy i dziewiąty punkt kontrolny. Dwunasty punkt kontrolny to punkt, w którym krzywa przecina linię łączącą dziewiąty i dziesiąty punkt kontrolny. Krzywą można narysować w dowolnej kolejności, ale nie wszystkie punkty są przydatne w praktyce. Punkty na początku i na końcu krzywej są zwykle najbardziej przydatne, ale mogą być również przydatne w środku krzywej. Algorytm krzywej Beziera jest prosty, ale można go użyć do stworzenia dowolnego kształtu.

Jak narysować krzywą w Svg?

Aby narysować krzywą w svg, musisz utworzyć element i zdefiniować na nim atrybut reklamy. Atrybut d definiuje dane ścieżki dla elementu. Dane ścieżki składają się z serii poleceń i parametrów. Każde polecenie składa się z litery i cyfry. Litery oznaczają polecenie, a liczba oznacza parametr. Polecenia rysowania krzywej to C, c, S, s, Q, q, T, t, A, a. Polecenie C oznacza „absolutną sześcienną krzywą Beziera”. Polecenie c oznacza „względną sześcienną krzywą Beziera”. Polecenie S oznacza „absolutnie gładką sześcienną krzywą Beziera”. Polecenie s oznacza „względnie gładką sześcienną krzywą Beziera”. Komenda Q oznacza „absolutną kwadratową krzywą Beziera”. Polecenie q oznacza „względną kwadratową krzywą Beziera”. Polecenie T oznacza „absolutnie gładką kwadratową krzywą Beziera”. Polecenie t oznacza „względnie gładką kwadratową krzywą Beziera”. Polecenie A oznacza „absolutny łuk eliptyczny”. Polecenie a oznacza „względny łuk eliptyczny”. Każde z tych poleceń ma inny zestaw parametrów definiujących krzywą.

Komenda sześciennej krzywej Beziera (C) będzie następująca: [code type=html]. To =1, =1, =1, =1, =1, =1, =1, =1, =1, =1, =1, =1, =1, =1 Krzywa zaczyna się w punkcie 100,200, dokąd prowadzi ścieżka. Drugi punkt kontrolny to 400,100. Krzywa ma na końcu wartość 400 200. Krzywe, podobnie jak linie, nie muszą być zakrzywione w sposób ciągły. Jeśli połączysz jedną krzywą z drugą, możesz tworzyć jeszcze bardziej złożone krzywe. Te polecenia, znane również jako S i S, są używane przez przeglądarki, aby ułatwić Ci znalezienie tego, czego szukasz.

Tym razem dwie krzywe są reprezentowane za pomocą skrótu bezwzględnego. Aby pracować z kwadratem Beziera , wymagany jest jeden punkt kontrolny zamiast dwóch. Polecenie arc uwzględnia większość parametrów. Istnieją trzy rodzaje poleceń dotyczących krzywych. Punkt początkowy i końcowy, elipsa z rotacją osi rx, ry i x oraz cztery łuki to wszystko możliwe. Łuki są używane do odzwierciedlenia obrazu flagi dużego łuku w obrazie flagi przeciągnięcia. Niebieski łuk reprezentuje czerwony łuk, który tworzy się wokół osi, gdy oba końce są skierowane w tym samym kierunku.

W rezultacie wartość 0 wskazuje, że należy użyć mniejszego łuku, a wartość 1 wskazuje, że należy użyć większego łuku. Ścieżka jest większa i potężniejsza niż podstawowy kształt. Można je stworzyć przy odrobinie większego wysiłku, ale niewiele. Masz duże szanse, że wszystkie edytory graficzne wyeksportują obraz jako ścieżkę. Najlepiej zapamiętać polecenia w ciągu kilku minut.

Dowiedz się, jak tworzyć ścieżki w Svg

Używając ścieżek w SVG, możesz tworzyć różnorodne kształty, w tym okręgi i krzywe. W tym artykule przyjrzymy się, jak używać tych poleceń do tworzenia tych tras.
Polecenia A można użyć do utworzenia łuku w SVG. Po otwarciu okna poleceń łuku będziesz mógł określić promień x i y okręgu lub elipsy, które zostaną użyte do wygenerowania łuku. Możesz także podać punkt początkowy i końcowy łuku, a także kąt, pod jakim ma być narysowany.
Polecenie C umożliwia również tworzenie zakrzywionych ścieżek. Jeśli go użyjesz, określa ścieżkę, którą należy narysować, a także elementy glif i brakujący glif. Definicja ścieżki to lista poleceń ścieżki, w której każde polecenie jest reprezentowane przez literę polecenia i liczbę reprezentującą jego parametry.
Na przykład, aby wyśrodkować ścieżkę w SVG, możesz użyć atrybutu viewBox. Wyśrodkuje ścieżkę w rzutni niezależnie od tego, gdzie znajduje się w dokumencie.

Svg Generator krzywej Beziera

Istnieje wiele generatorów krzywych Beziera svg dostępnych online. Te generatory umożliwiają tworzenie niestandardowych krzywych Beziera svg na podstawie określonych parametrów. Możesz kontrolować szerokość, wysokość, liczbę punktów kontrolnych i inne aspekty krzywej. Te generatory mogą być świetnym sposobem na tworzenie niestandardowych kształtów i projektów dla projektów internetowych.

Krzywa ścieżki SVG

Krzywe ścieżki SVG służą do tworzenia gładkich krzywych na ścieżce SVG. Dostępne są cztery rodzaje krzywych: krzywe kwadratowe, krzywe sześcienne, krzywe łukowe i krzywe gładkie. Każdy typ krzywej ma swoje zalety i wady, dlatego ważne jest, aby wybrać odpowiedni typ krzywej do danego zadania. Krzywe kwadratowe są najprostszym rodzajem krzywych i są łatwe do tworzenia i manipulowania. Krzywe sześcienne są bardziej złożone i można ich używać do tworzenia bardziej szczegółowych kształtów. Krzywe łukowe najlepiej nadają się do tworzenia okrągłych lub eliptycznych kształtów. Gładkie krzywe są kombinacją pozostałych trzech typów krzywych i mogą być używane do tworzenia różnorodnych kształtów.

Ścieżka to geometria obrysu obiektu zdefiniowana przez przesunięcie kształtu obiektu na jedną stronę, linię do, krzywą do (zarówno sześciennych, jak i kwadratowych nachyleń), łuki i bliskie ścieżki. Ścieżki złożone (tj. ścieżki z wieloma ścieżkami podrzędnymi) mogą być używane, aby obiekty miały dziury pierścieniowe. Opisuje składnię, zachowanie i interfejsy DOM ścieżek SVG oraz sposób ich wyrażania. Każde polecenie w sekwencji danych ścieżki następuje po pojedynczym znaku. Składnia danych ścieżki jest zwięzła, aby umożliwić minimalny rozmiar pliku, a jednocześnie umożliwić wydajne pobieranie. Dane ścieżki można podzielić na wiele wierszy, aby poprawić ich czytelność, ponieważ zawarte w nich znaki zawierają znaki nowej linii. Wykorzystując znormalizowany znak spacji w znacznikach, nowe wiersze w nazwach atrybutów zostaną znormalizowane.

Ta wartość reprezentuje kształt określony przez ciąg danych ścieżki. Błędy w ciągu znaków są obsługiwane zgodnie z sekcją Obsługa błędów danych ścieżki danych ścieżki. Segmenty danych ścieżki (jeśli istnieją) muszą zaczynać się od polecenia moveto (jeśli istnieje). Linie proste są rysowane automatycznie od bieżącego punktu do punktu początkowego bieżącej ścieżki podrzędnej. Możliwe, że ten odcinek ścieżki jest pozbawiony dowolnej długości. Ścieżka bliższa jest zdefiniowana jako ścieżka, która jest połączona przez początek segmentu początkowego przy użyciu wartości „połączenia linii obrysu” na końcu segmentu końcowego. Gdy pierwszy i ostatni segment ścieżki nie są połączone, istnieje różnica między zamkniętą ścieżką podrzędną a otwartą ścieżką podrzędną.

Python nie obsługuje obecnie operacji zamykania ścieżki zamykania segmentów jako polecenia. Aby zmienić punkty odniesienia, linia dowodzenia może rysować proste linie od jednego punktu do drugiego. Gdy polecenie względne l jest używane do generowania linii, punktem końcowym jest (cpy x). Aby narysować linię poziomą w kierunku dodatniej osi x, użyj polecenia względnego h z dodatnią wartością x. Pierwsze pięć przykładów pokazuje pojedynczy segment sześcienny ścieżki Beziera . W porządku malejącym możesz zarządzić łuk eliptyczny. Jeśli używasz polecenia względnego, łuk jest reprezentowany przez współrzędne (cxy).

Flagi duże i rozciągnięte wskazują liczbę narysowanych łuków, jak pokazano na poniższym diagramie. Przetwarzanie EBNF musi pochłonąć jak najwięcej danej produkcji, aby zatrzymać się w punkcie, w którym postać nie spełnia już wymagań dla tej produkcji. Gdy wartość właściwości d wynosi zero, renderowanie jest wyłączone. Podczas obliczania kształtu zakończenia i wyświetlania znaczników na granicach segmentów włączone jest zastąpienie granic segmentów. Jeśli zarówno rx, jak i ry są równe zeru, ten łuk zostanie uznany za odcinek linii prostej (linia łącząca punkty końcowe). Aby uzyskać więcej informacji na temat tej operacji skalowania, zobacz sekcję dodatku dotyczącą formuły matematycznej. Segmenty ścieżki o zerowej długości nie są nieprawidłowe i będą miały wpływ na renderowanie w następujących przypadkach.

Dodając atrybut „pathLength” do ścieżki, autor może obliczyć całkowitą długość ścieżki, aby klient użytkownika mógł obliczyć odległość wzdłuż ścieżki. Operację przenoszenia w elemencie „ścieżka” można uznać za operację o zerowej długości. Do obliczenia długości ścieżki można użyć tylko kilku linii, krzywych i strzałek.

Ścieżki, krzywe i łuki: podstawy elementu ścieżki

Ścieżki są zwykle definiowane za pomocą elementów „liniowych”, z których można utworzyć linię prostą. Ponadto element „curve” może być używany do wypełniania krzywych elementami „fill” lub „stroke”.
Jeśli chcesz utworzyć ścieżkę przechodzącą przez kilka różnych punktów, możesz użyć elementu „arc”. Element „arc” ma dwie cechy: punkt początkowy i punkt końcowy. Rozmiar łuku można również określić, określając jego promień.
Wreszcie, kształty mogą być używane do tworzenia ścieżek. Element „ścieżka” składa się z dwóch elementów: punktu początkowego i punktu końcowego. Atrybut degree, znany również jako element reklamy, jest zawarty jako część elementu ścieżki. Tutaj określa się stopień ruchu ścieżki wokół kształtu.
W rezultacie istnieje wiele sposobów korzystania ze ścieżki, a wszystkie jej składniki są podsumowane w elemencie „ścieżka”. Ponieważ element path zawiera jeden atrybut, atrybut „d”, który mówi mu, jaki kształt ma narysować, pamiętaj, że zawiera on jeden atrybut.

Przykład ścieżki Svg

Ścieżki SVG definiują kształt obiektu jako serię połączonych linii i krzywych. Przykład ścieżki svg definiuje kształt serca.

Element ścieżki jest ostatnim elementem rysunku. Atrybut d jest wymagany do opisania tego, co rysuje. Jest w nim wiele funkcjonalności, ale w większości jest to tylko mini składnia z łatwo zauważalną nieczytelną wartością. Możemy ponownie sformatować kod, aby nadać mu sens (nadal ma on oryginalny charakter). Ścieżkę można wykorzystać do narysowania linii prostej z powrotem do punktu, w którym ustawiono pióro, dzięki czemu jest to tania i prosta metoda. Ścieżka musi być zamknięta przez Z (lub z, to nie ma znaczenia), tak jak każde inne polecenie i jest to polecenie opcjonalne. Komenda A jest zdecydowanie najtrudniejsza. Aby określić szerokość, wysokość i obrót owalu, należy określić, jaką ścieżkę ma on podążać. Istnieją dwie możliwe elipsy, którymi może podążać ścieżka, dwie różne ścieżki dla każdej elipsy i cztery różne ścieżki dla każdej elipsy.

Beziery sześcienne

Sześcienna krzywa Beziera jest krzywą parametryczną często używaną w grafice komputerowej i dziedzinach pokrewnych. Krzywa jest zdefiniowana przez cztery punkty: dwa punkty końcowe i dwa punkty kontrolne. Krzywe Beziera można łączyć, tworząc splajn Beziera, który jest krzywą zdefiniowaną fragmentarycznie, składającą się z wielu krzywych Beziera połączonych końcami.

Zapoznaj się z matematyką stojącą za krzywą Beziera i jej powiązaniem z innymi funkcjami czasowymi w tym filmie. Możesz dostosować swoją wizualizację, aby odzwierciedlała matematykę stojącą za tymi pięknymi przejściami, korzystając z interaktywnej wizualizacji. Krzywa jest specjalnym rodzajem krzywej, której można użyć do zobrazowania procesu przechodzenia z jednego stanu do drugiego. Możemy teraz kolejno przemieszczać się pomiędzy segmentami na osi P0 -> P1, a także P1 -> P2. Ścieżkę przypominającą kwadratową krzywą Beziera można uzyskać, jeśli połączymy te dwa punkty odcinkiem i umieścimy na nim interpolowany punkt (niebieska kropka). Nazywa się to interpolacją liniową. Zaczynając od punktów kontrolnych P0, P1, P2 i P3, użyjemy wzoru do przedstawienia krzywej sześciennej beziera.

Kiedy dodamy czwarty punkt – P4 – do każdego segmentu łączącego cztery punkty, otrzymamy interpolowany punkt między segmentami. W rezultacie łączymy te punkty i tworzymy (*)interpolowany (*) punkt dla każdego nowego segmentu (zielony). Następnym krokiem jest połączenie kropek i narysowanie odcinka każdego punktu. Na koniec mamy wzór na narysowanie krzywej. Poniżej przedstawiono kilka sposobów wyrażania formuły cubebeziera. ( P0, P1, P2, P3) = dla (niech t = 0, t = 1 <= 1); t = 1 Innymi słowy, równanie ma 1 dla 60. res.

push (x: valX, y: valY); rez. Współrzędne P1 i P2 reprezentują ruch elementu, a kiedy przechodzi, podąża za tą krzywą. W ten sposób koncepcja matematyczna przekształca się w ruch. Użycie określonych krzywych z określonym przejściem sześciennym beziera może być użyte do przedstawienia różnych przejść łatwości. Dla wygody wszystkie te funkcje synchronizacji są dostarczane przez CSS. Framer Motion odkrył, że istnieje silny związek między funkcjami wygładzania i imigracji w obiekcie przejścia. Funkcja sześciennego Beziera w Framing Motion znacznie różni się od tego, co widzieliśmy w CSS.

Wartość twoich punktów P1 i P2, odpowiednio, musi zostać przekazana do właściwości łatwości, aby opisać to przejście. Ten post na blogu dostarczył fascynujących informacji na temat niektórych fajnych rzeczy, których używamy na co dzień, i mam nadzieję, że wzbudził Twoje zainteresowanie. Mając większą wiedzę na temat funkcji sześciennej-Beziera i instrukcji, będziesz w stanie z łatwością tworzyć nowe przejścia i animacje.