Curvas SVG e curvas de Bezier: como calculá-las

Uma curva SVG é uma curva suave contínua. Ele pode ser usado para criar linhas, curvas, arcos e muito mais. Mais importante ainda, pode ser usado para criar curvas bezier . Uma curva bezier é uma curva definida por quatro pontos. Os dois primeiros pontos são os pontos inicial e final da curva e os dois últimos pontos são os pontos de controle. Os pontos de controle determinam a forma da curva. Existem muitas maneiras de calcular uma curva de Bézier. A forma mais comum é usar o algoritmo de De Casteljau. Este algoritmo é usado para calcular pontos em uma curva de Bezier. O algoritmo de De Casteljau é um algoritmo recursivo. Isso significa que ele divide o problema em subproblemas menores. O algoritmo começa com os quatro pontos que definem a curva de Bezier. Em seguida, calcula o ponto médio entre os pontos inicial e final. Este ponto médio é então usado para calcular o próximo ponto na curva. Este processo é repetido até que o número desejado de pontos seja atingido. O algoritmo de De Casteljau não é a única forma de calcular uma curva de Bezier. Existem outros métodos, como o uso de B-splines. No entanto, o algoritmo de De Casteljau é o método mais comum e é o mais utilizado.

Esta é uma continuação da minha postagem anterior no blog sobre gráficos vetoriais. Manipulação e animação são fáceis de fazer com SVGs porque são leves, rápidos e naturais. Voltaremos ao tema da sequência de retas e curvas com a ajuda de algumas ilustrações. as curvas de Bezier foram originalmente nomeadas em homenagem a dois engenheiros franceses e foram formalmente adaptadas por eles. Eles são classificados como pontos de controle absolutos ou relativos, dependendo do contexto. Quando o botão do mouse é pressionado, a mira do evento mouseDown aparece e os pontos indicam onde as linhas horizontais e verticais do evento mouseDown se cruzam com a curva na tela. Os pontos de controle agora podem ser editados em editores de gráficos vetoriais, como o Illustrator, que se tornou uma parte intuitiva da experiência do usuário.

Esta ação está ocorrendo principalmente em utilitários/bezierIntersections.js. Pode haver até três raízes cúbicas, e algumas delas podem ser coordenadas inúteis para raízes fora de especificação em segmentos de curva mais planos. Para encontrar a interseção de curvas e linhas, usamos as definições de curvas/linhas. Como o código é uma demonstração, não limpei as coordenadas inúteis; em vez disso, concentrei-me na álgebra porque o código é apenas uma demonstração.

Use a fórmula (1-t)P0 + (t)P1 se quiser encontrar qualquer ponto P ao longo de uma linha: P0 é o ponto inicial e P1 é o ponto final.

Como as curvas de Bezier são calculadas?

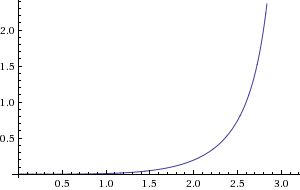
As curvas de Bezier são calculadas usando uma equação paramétrica para definir uma curva. A equação paramétrica define as coordenadas x e y da curva em função de um parâmetro t. O parâmetro t pode ser qualquer número real entre 0 e 1. Quando t é 0, as coordenadas xey da curva são as coordenadas xey do primeiro ponto de controle. Quando t é 1, as coordenadas x e y da curva são as coordenadas x e y do último ponto de controle. Para valores de t entre 0 e 1, as coordenadas x e y da curva estão em algum lugar entre as coordenadas x e y do primeiro e do último ponto de controle.

Um recurso frequentemente usado em gráficos de computador é o uso de curvas chanfradas. Eles podem ser definidos por polinômios de Bernstein (t = (1 – t))*n = 1. Em Python, podemos calcular a curva do intervalo[0, 1]. Como a forma da curva é completamente determinada por P1 em 0 a 1, ela pode ser de 0 a 1. Uma multiplicação de matriz pode ser usada para representar a fórmula de Bezier. Cada polinômio é uma função de dois Pis na matriz, com os coeficientes da matriz todos centrados neles. Desta forma, podemos programar a versão geral da curva para qualquer número de pontos de controle usando a eq. Desenhe uma curva suave com a ajuda de um conjunto de pontos.

Quando o vetor tangente é desenhado com pontos de controle em (x0, y0), (x1, y1), (x2, y2), (x3, y3) e (x4, y4), cada ponto no vetor tangente tem o mesmo direção. Uma curva de Bezier é formada pela casca convexa de pontos. Um quadrilátero com vértices em (x0, y0), (x1, y1), (x2, y2) e (x3, y3) é o resultado de uma curva de quadratura com quatro pontos. As seguintes equações são usadas para definir o casco convexo. Uma raiz quadrada de * x0)2 é igual a uma raiz quadrada de * x0. (y) = b0)2. Para uma equação de curva de Bezier , aqui está o que você deve fazer. Em outras palavras, =. É igual a (x x0)2). (02) Y=0) é a combinação mais adequada. B0,3 é uma unidade de (1*u)3. O valor =. Uma raiz quadrada de (x x0)2 é igual a uma raiz quadrada de (x x0).2). (Y0) 2 é a fórmula para isso. (x x0)2) é um valor que denota a soma de dois números adjacentes. Quando se trata de y (y y0), devemos usar (y y0). Pois (x * x0)2) é igual a (x * x0). = (x0 x1)2 + (y0 y1)2 = br>. 1,3=3u(1*u)2 é uma unidade de medida. B3,=3u2,(1*u) é um tipo de unidade de medida em matemática.

Como funciona o caminho SVG?

O *path É capaz de desenhar linhas, curvas, arcos e outras formas. Um caminho pode ser composto de várias linhas retas ou linhas curvas, resultando em formas complexas. Formas complexas compostas apenas por linhas retas podem ser geradas como s.

Um único número ou letra em um caminho SVG pode parecer intimidador; no entanto, há muitos números e letras nos arquivos. Nesta lição, usaremos um caminho para desenhar um retângulo e usaremos uma ferramenta de desenho para fazer isso. O Codepen ou qualquer outra ferramenta que permita ver rapidamente quais alterações estão sendo feitas é um bom lugar para começar a codificar. Apesar de nossos melhores esforços, podemos facilitar as coisas para eles. Como resultado, ao desenhar nosso lado direito de nosso retângulo, queremos que nosso lápis permaneça no eixo x enquanto sobe 200 no y. Y -200 é adicionado à equação para mover para cima. Em seguida, podemos usar o comando z para retornar uma linha à sua posição original.

Caminhos Svg e CSS

Meu caminho é um símbolo. Altura: 100px; width:115br> Uma largura de 100px é igual a uma largura de *br.
svg path=”M10,L20″ *br Mypath %22br%22 Para exibir esta imagem, habilite height:100px. Clique duas vezes em *br> para exibir esta largura. Mypath é um diretório ativo.
Plano de fundo: #FFF, *br*.

Como são calculados os pontos de controle de Bezier?

Não há uma resposta definitiva para esta questão, pois há uma variedade de maneiras pelas quais os pontos de controle Bezier podem ser calculados, dependendo do resultado desejado. Alguns métodos comuns incluem o uso das bissetrizes das linhas que conectam os pontos finais da curva ou a solução de um sistema de equações que leva em consideração as propriedades desejadas da curva. Em geral, no entanto, os pontos de controle são normalmente escolhidos para criar uma curva suave que passa pelos pontos finais fornecidos.

Na programação, as curvas bezier são um recurso bem conhecido. Eles são usados ​​em gráficos para criar gráficos vetoriais escaláveis ​​de curvas, garantindo que a curva permaneça suave à medida que se move pela curva. Você deve conhecer quatro pontos para desenhar a Curva de Bezier: o ponto inicial, o ponto final e dois pontos de controle. A distância entre o ponto inicial e os pontos de controle, com base em um caminho percentual longo, é usada para calcular a Curva de Bezier. Para o ponto médio de dois pontos, multiplique M por P0 e P1. Não consigo explicar tão bem quanto o vídeo do YouTube, então assista se quiser saber mais. A fórmula para encontrar o valor de um ponto P ao longo de uma curva de Bezier é dada abaixo.

As três unidades básicas de medida são P0 (o ponto), P (o ponto ao longo da linha) e T (a porcentagem ao longo da linha). P1 = (o ponto final desconhecido) é a fórmula para encontrar esse número. A razão é 1 – p (t) – 0 / p.

O vetor tangente à curva de Bezier no início (parada) é perpendicular à linha que conecta os dois primeiros (os dois últimos). Há um vetor tangente à curva de Bezier no início (parada), mas a curva é inclinada para a direita. É impossível gerar uma curva de Bezier manualmente com um algoritmo recursivo. O sistema começa com o primeiro ponto de controle e termina com uma curva que passa pelo próximo ponto de controle. É simples de usar, mas também pode ser usado para fazer curvas de qualquer ordem. Em geral, a curva começa no primeiro ponto de controle. No segundo ponto, a curva cruza o eixo y. Finalmente, a curva cruza o eixo x em seu terceiro ponto. O quarto ponto de controle está localizado no ponto onde a curva intercepta a linha que conecta os dois primeiros pontos de controle. Um quinto ponto de controle está no ponto onde a curva cruza com a linha que conecta o segundo e o terceiro pontos de controle. O sexto ponto de controle conecta o terceiro e o quarto pontos de controle porque é o ponto onde a curva intercepta a linha. O sétimo ponto de controle é o ponto no qual a curva intercepta a linha que conecta o quarto e o quinto pontos de controle. O oitavo ponto de controle é o ponto no qual a curva cruza com a linha que conecta o quinto e o sexto pontos de controle. O nono ponto de controle é o ponto onde a curva intercepta a linha que conecta o sexto e o sétimo pontos de controle. Quando a curva intercepta a linha que conecta o sétimo e o oitavo pontos de controle, os décimos pontos de controle são definidos. Os pontos de controle estão localizados no décimo primeiro e nono pontos de controle, respectivamente, no ponto onde a curva cruza com a linha que conecta o oitavo e o nono pontos de controle. O décimo segundo ponto de controle é o ponto no qual a curva intercepta a linha que conecta o nono e o décimo pontos de controle. A curva pode ser desenhada em qualquer ordem, mas nem todos os pontos são úteis na prática. Os pontos no início e no final de uma curva são normalmente os mais úteis, mas também podem ser úteis no centro da curva. O algoritmo da curva de Bezier é direto, mas você pode usá-lo para criar qualquer forma.

Como você desenha uma curva em Svg?

Para desenhar uma curva em svg, você precisa criar um elemento e definir o atributo de anúncio nele. O atributo d define os dados do caminho para o elemento. Os dados do caminho consistem em uma série de comandos e parâmetros. Cada comando consiste em uma letra e um número. As letras representam o comando e o número representa o parâmetro. Os comandos para desenhar uma curva são C, c, S, s, Q, q, T, t, A, a. O comando C significa “curva cúbica absoluta de Bezier”. O comando c significa “curva cúbica relativa de Bezier”. O comando S significa “curva de Bezier cúbica suave absoluta”. O comando s significa “curva de Bezier cúbica suave relativa”. O comando Q significa “curva de Bezier quadrática absoluta”. O comando q significa “curva quadrática relativa de Bezier”. O comando T significa “curva de Bézier quadrática suave absoluta”. O comando t significa “curva de Bézier quadrática suave relativa”. O comando A significa “arco elíptico absoluto”. O comando a significa “arco elíptico relativo”. Cada um desses comandos possui um conjunto diferente de parâmetros que definem a curva.

O comando da curva cúbica de Bezier (C) será o seguinte: [code type=html]. É =1, =1, =1, =1, =1, =1, =1, =1, =1, =1, =1, =1, =1, =1 A curva começa no ponto 100.200, onde o caminho continua. O segundo ponto de controle é 400.100. A curva tem um valor de 400.200 no final. Curvas, como linhas, não precisam ser curvas continuamente. Se você conectar uma curva a outra, poderá criar curvas ainda mais complexas. Esses comandos, também conhecidos como S e S, são usados ​​pelos navegadores para facilitar a localização do que você está procurando.

Desta vez, as duas curvas são representadas usando o atalho absoluto. Para trabalhar com bézier quadrático , é necessário um ponto de controle em vez de dois. Com o comando arc, a maioria dos parâmetros são levados em consideração. Existem três tipos de comandos de curva. Um ponto inicial e final, uma elipse com rotação dos eixos rx, ry e x e quatro arcos são possibilidades. Os arcos são usados ​​para espelhar a imagem do sinalizador de arco grande na imagem do sinalizador de varredura. O arco azul representa o arco vermelho que se forma ao redor do eixo quando ambas as extremidades apontam na mesma direção.

Como resultado, um valor de 0 indica que o arco menor deve ser usado, enquanto um valor de 1 indica que o arco maior deve ser usado. O caminho é maior e mais poderoso do que a forma básica. Eles podem ser criados com um pouco mais de esforço, mas não muito. Você tem uma boa chance de que todos os editores gráficos exportem uma imagem como um caminho. É melhor memorizar os comandos em questão de minutos.

Aprenda a criar caminhos em SVG

Usando Caminhos em SVG, você pode criar uma variedade de formas, incluindo círculos e curvas. Neste artigo, veremos como usar esses comandos para criar essas rotas.
O comando A pode ser usado para criar um arco em SVG. Depois de abrir a janela de comando do arco, você poderá especificar os raios x e y do círculo ou elipse que serão usados ​​para gerar o arco. Você também pode incluir os pontos inicial e final do arco, bem como o ângulo em que deve ser desenhado.
O comando C também permite criar caminhos curvos. Se você usá-lo, ele especifica um caminho que deve ser desenhado, bem como os elementos glyph e missingglyph. A definição de caminho é uma lista de comandos de caminho, na qual cada comando é representado por uma letra de comando e um número que representa seus parâmetros.
Para centralizar um caminho em SVG, por exemplo, você pode usar o atributo viewBox. Ele centralizará o caminho na viewport, independentemente de onde ele se encontre no documento.

Gerador de Curvas Svg Bezier

Existem vários geradores de curvas svg bezier disponíveis online. Esses geradores permitem que você crie uma curva svg bezier personalizada com base nos parâmetros especificados. Você pode controlar a largura, altura, número de pontos de controle e outros aspectos da curva. Esses geradores podem ser uma ótima maneira de criar formas e designs personalizados para seus projetos da web.

Curva de Caminho Svg

Curvas de caminho SVG são usadas para criar curvas suaves em um caminho SVG. Existem quatro tipos de curvas disponíveis: curvas quadráticas, curvas cúbicas, curvas de arco e curvas suaves. Cada tipo de curva tem suas próprias vantagens e desvantagens, por isso é importante escolher o tipo certo de curva para a tarefa em questão. Curvas quadráticas são o tipo mais simples de curva e são fáceis de criar e manipular. As curvas cúbicas são mais complexas e podem ser usadas para criar formas mais detalhadas. As curvas de arco são mais adequadas para criar formas circulares ou elípticas. As curvas suaves são uma combinação dos outros três tipos de curvas e podem ser usadas para criar uma variedade de formas.

Um caminho é a geometria do contorno de um objeto que é definido movendo a forma do objeto para um lado, linha para, curva para (inclinações cúbicas e quadráticas), arcos e caminhos próximos. Caminhos compostos (ou seja, caminhos com vários subcaminhos) podem ser usados ​​para permitir que os objetos tenham orifícios de rosca. Ele descreve a sintaxe, o comportamento e as interfaces DOM dos caminhos SVG e como eles são expressos. Cada comando na sequência de dados do caminho segue um único caractere. A sintaxe dos dados do caminho é concisa para permitir um tamanho de arquivo mínimo e, ao mesmo tempo, permitir downloads eficientes. Os dados do caminho podem ser divididos em várias linhas para melhorar sua legibilidade porque os caracteres nele contêm caracteres de nova linha. Aproveitando um caractere de espaço normalizado na marcação, novas linhas em nomes de atributos serão normalizadas.

Esse valor representa a forma especificada por uma string de dados de caminho. Os erros dentro de uma string são tratados de acordo com a seção Tratamento de Erros de Dados de Caminho dos Dados de Caminho. Segmentos de dados de caminho (se houver) devem começar com um comando moveto (se houver). Linhas retas são desenhadas do ponto atual para o ponto inicial do subcaminho atual automaticamente. É possível que este segmento de caminho seja desprovido de qualquer comprimento. Closepath é definido como um caminho que é unido pelo início do segmento inicial usando o valor 'stroke-linejoin' no final do segmento final. Quando o primeiro e o último segmento de caminho não são unidos, há uma diferença entre um subcaminho fechado e um subcaminho aberto.

Atualmente, o Python não oferece suporte a operações de caminho fechado de conclusão de segmento como um comando. Para alterar os pontos de referência, uma linha de comando pode traçar linhas retas de um ponto a outro. Quando um comando l relativo é usado para gerar uma linha, o ponto final é (cpy x). Para desenhar uma linha horizontal na direção do eixo x positivo, use um comando h relativo com um valor x positivo. Os primeiros cinco exemplos demonstram um único segmento cúbico do caminho de Bezier . Em ordem decrescente, você pode comandar um arco elíptico. Se você usar um comando relativo, o arco é representado pelas coordenadas (cxy).

Os flags large e sweep indicam o número de arcos desenhados, conforme mostrado no diagrama abaixo. O processamento de EBNF deve consumir o máximo possível de uma determinada produção para parar no ponto em que um personagem não atende mais aos requisitos para essa produção. Quando o valor da propriedade d é zero, a renderização é desabilitada. Ao calcular a forma da tampa e exibir marcadores nos limites do segmento, uma substituição é habilitada para os limites do segmento. Se rx e ry forem zero, este arco será considerado um segmento de linha reta (uma linha para conectar os pontos finais). Para obter mais informações sobre esta operação de dimensionamento, consulte a seção do apêndice para a fórmula matemática. Segmentos de caminho com comprimento zero não são inválidos e terão efeito na renderização nos seguintes casos.

Ao adicionar o atributo 'pathLength' ao caminho, o autor pode calcular o comprimento total do caminho para que o agente do usuário possa calcular a distância ao longo de um caminho. Uma operação de movimento dentro de um elemento 'path' pode ser considerada uma operação de comprimento zero. Apenas algumas linhas, curvas e setas podem ser usadas para calcular o comprimento do caminho.

Caminhos, curvas e arcos: o básico do elemento Path

Caminhos são tipicamente definidos usando elementos 'line', e uma linha reta pode ser criada com eles. Além disso, o elemento 'curve' pode ser usado para preencher curvas com elementos 'fill' ou 'stroke'.
Se você deseja criar um caminho que passe por alguns pontos diferentes, pode usar o elemento 'arco'. O elemento 'arco' tem duas características: um ponto inicial e um ponto final. O tamanho do arco também pode ser especificado especificando seu raio.
Finalmente, as formas podem ser usadas para criar caminhos. Existem dois elementos no elemento 'path': o ponto inicial e o ponto final. Um atributo de grau, também conhecido como elemento ad, é incluído como parte do elemento path. O grau de movimento de um caminho ao redor da forma é especificado aqui.
Como resultado, existem várias maneiras de usar um caminho e todos os seus componentes são resumidos no elemento 'caminho'. Como o elemento path contém um único atributo, o atributo 'd', que informa qual forma desenhar, lembre-se de que ele contém um único atributo.

Exemplo de caminho SVG

Os caminhos SVG definem a forma de um objeto como uma série de linhas e curvas conectadas. O exemplo de caminho svg define a forma de um coração.

O elemento de caminho é o elemento final em um desenho. O atributo d é necessário para descrever o que desenha. Há muita funcionalidade nele, mas é principalmente apenas uma mini sintaxe com um valor indecifrável facilmente discernível. Podemos reformatar o código para entendê-lo (ele ainda tem o caractere original). Um caminho pode ser usado para traçar uma linha reta de volta ao ponto onde a caneta foi montada, tornando-se um método simples e barato. O caminho deve ser fechado por Z (ou z, não importa) como qualquer outro comando, e é um comando opcional. O comando A, de longe, é o mais difícil. Para determinar a largura, a altura e a rotação de uma oval, especifique o caminho que ela deve seguir. Existem duas elipses possíveis para o caminho percorrer, dois caminhos diferentes para cada elipse e quatro caminhos diferentes para cada elipse.

Beziers Cúbicos

Uma curva cúbica de Bezier é uma curva paramétrica frequentemente usada em computação gráfica e campos relacionados. A curva é definida por quatro pontos: dois pontos finais e dois pontos de controle. As curvas de Bezier podem ser combinadas para formar uma spline de Bezier, que é uma curva definida por partes que consiste em várias curvas de Bezier unidas de ponta a ponta.

Entenda a matemática por trás de uma curva de Bezier e como ela se relaciona com outras funções de tempo neste vídeo. Você pode personalizar sua visualização para refletir a matemática por trás dessas belas transições usando a visualização interativa. A curva é um tipo especial de curva que pode ser usada para representar o processo de mudança de um estado para o outro. Agora podemos mover sucessivamente entre os segmentos no eixo P0 -> P1, bem como P1 -> P2. Um caminho semelhante a uma curva quadrática de Bezier pode ser obtido se ligarmos esses dois pontos com um segmento e posicionarmos um ponto interpolado (o ponto azul) sobre ele. É conhecida como interpolação linear. Começando com os pontos de controle P0, P1, P2 e P3, usaremos uma fórmula para representar uma curva cubo-bezier.

Quando adicionamos o quarto ponto – P4 – a cada segmento que liga os quatro pontos, obtemos um ponto interpolado entre os segmentos. Como resultado, ligamos esses pontos e criamos um ponto (*)interpolado (*) para cada novo segmento (verde). O próximo passo é ligar os pontos e desenhar um segmento de cada ponto. Finalmente, temos uma fórmula para desenhar a curva. A seguir estão algumas maneiras de expressar a fórmula cubebezier. ( P0, P1, P2, P3) = for (let t = 0, t = 1 <= 1); t = 1 Em outras palavras, a equação tem um 1 para 60. res.

push ( x: valX, y: valY ); res. As coordenadas P1 e P2 representam o movimento de um elemento e, quando transita, segue esta curva. É assim que o conceito matemático se transforma em movimento. O uso de curvas específicas com uma transição cubebezier específica pode ser usado para representar uma variedade de transições de facilidade. Por uma questão de conveniência, todas essas funções de temporização são fornecidas pelo CSS. A Framer Motion descobriu que há uma forte relação entre as funções easing e immigrate no objeto de transição. A função cubic-bezier no Framing Motion é significativamente diferente do que vimos no CSS.

O valor de seus pontos P1 e P2, respectivamente, deve ser passado para a propriedade de facilidade para descrever essa transição. Esta postagem do blog forneceu a você alguns insights fascinantes sobre algumas das coisas legais que usamos diariamente e espero que tenha despertado seu interesse. Com mais conhecimento da função cubicbezier e das instruções, você poderá criar novas transições e animações com facilidade.