การคำนวณสหสัมพันธ์ใน Excel: คู่มือวิธีการของคุณ

Microsoft Excel ให้คุณทำมากกว่าแค่สร้างสเปรดชีต — คุณยังสามารถใช้ซอฟต์แวร์เพื่อคำนวณฟังก์ชันหลัก เช่น ความสัมพันธ์ระหว่างสองตัวแปร ค่าสัมประสิทธิ์สหสัมพันธ์ที่เรียกว่าค่าสัมประสิทธิ์สหสัมพันธ์ เมตริกนี้มีประโยชน์สำหรับการวัดผลกระทบของการดำเนินการหนึ่งต่อการดำเนินการอื่นเพื่อแจ้งการดำเนินธุรกิจ

ไม่มั่นใจในทักษะ Excel ของคุณ? ไม่มีปัญหา. ต่อไปนี้คือวิธีการคำนวณและทำความเข้าใจค่าสัมประสิทธิ์สหสัมพันธ์ใน Excel

ค่าสัมประสิทธิ์สหสัมพันธ์ +1 บ่งชี้ถึง "ความสัมพันธ์เชิงบวกที่สมบูรณ์แบบ" ซึ่งหมายความว่าเมื่อตัวแปร X เพิ่มขึ้น ตัวแปร Y จะเพิ่มขึ้นในอัตราเดียวกัน ค่าสหสัมพันธ์ของ -1 ในขณะเดียวกันคือ "ความสัมพันธ์เชิงลบที่สมบูรณ์แบบ" ซึ่งหมายความว่าเมื่อตัวแปร X เพิ่มขึ้น ตัวแปร Y จะลดลงในอัตราเดียวกัน การวิเคราะห์สหสัมพันธ์อาจส่งกลับผลลัพธ์ที่ใดก็ได้ระหว่าง -1 ถึง +1 ซึ่งบ่งชี้ว่าตัวแปรเปลี่ยนแปลงในอัตราที่ใกล้เคียงกันแต่ไม่เหมือนกัน

ค่าสหสัมพันธ์สามารถช่วยให้ธุรกิจประเมินผลกระทบของการดำเนินการเฉพาะต่อการดำเนินการอื่นๆ ตัวอย่างเช่น บริษัทต่างๆ อาจพบว่าการใช้จ่ายด้านการตลาดบนโซเชียลมีเดียเพิ่มขึ้น การมีส่วนร่วมของลูกค้าก็เพิ่มขึ้นเช่นกัน ซึ่งบ่งชี้ว่าการใช้จ่ายที่มากขึ้นอาจสมเหตุสมผล

หรือพวกเขาอาจพบว่าแคมเปญโฆษณาเฉพาะส่งผลให้การมีส่วนร่วมของลูกค้าลดลงซึ่งสัมพันธ์กัน ซึ่งส่งผลให้จำเป็นต้องประเมินความพยายามในปัจจุบันอีกครั้ง การค้นพบว่าตัวแปรไม่มีความสัมพันธ์กันก็สามารถมีค่าได้เช่นกัน แม้ว่าสามัญสำนึกอาจแนะนำว่าฟังก์ชันหรือคุณลักษณะใหม่ในผลิตภัณฑ์ของคุณจะสัมพันธ์กับการมีส่วนร่วมที่เพิ่มขึ้น แต่ก็อาจไม่มีผลกระทบที่วัดได้ การวิเคราะห์สหสัมพันธ์ช่วยให้บริษัทต่างๆ สามารถดูความสัมพันธ์นี้ (หรือขาดความสัมพันธ์นี้) และทำการตัดสินใจเชิงกลยุทธ์ที่ดีได้

คุณจะคำนวณค่าสัมประสิทธิ์การแก้ไขใน Excel ได้อย่างไร? เรียบง่าย! ทำตามขั้นตอนเหล่านี้:

1. เปิด Excel

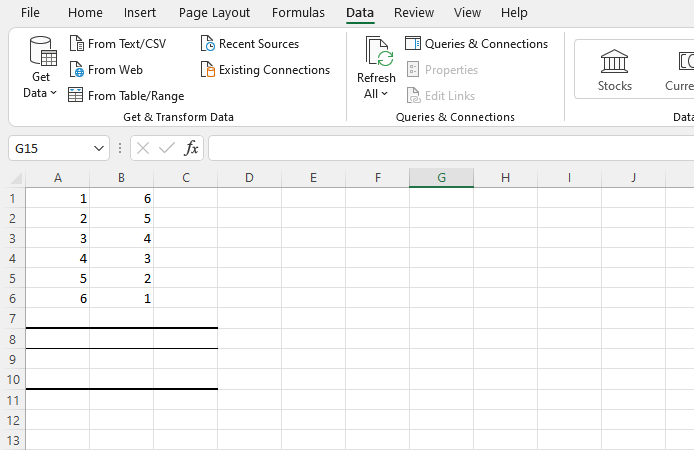
ขั้นตอนที่หนึ่ง: เปิด Excel และเริ่มเวิร์กชีตใหม่สำหรับข้อมูลตัวแปรที่สัมพันธ์กัน ป้อนจุดข้อมูลของตัวแปรแรกในคอลัมน์ A และตัวแปรที่สองในคอลัมน์ B คุณสามารถเพิ่มตัวแปรเพิ่มเติมได้เช่นกันในคอลัมน์ C, D, E เป็นต้น — Excel จะให้ค่าสัมประสิทธิ์สหสัมพันธ์สำหรับแต่ละรายการ

ในตัวอย่างด้านล่าง เราได้ป้อนข้อมูลหกแถวในคอลัมน์ A และหกแถวในคอลัมน์ B

2. ติดตั้ง Analysis Toolpak

ต่อไป? หากคุณไม่มี ให้ติดตั้ง Excel Analysis Toolpak

เลือก "ไฟล์" จากนั้นเลือก "ตัวเลือก" แล้วคุณจะเห็นหน้าจอนี้:

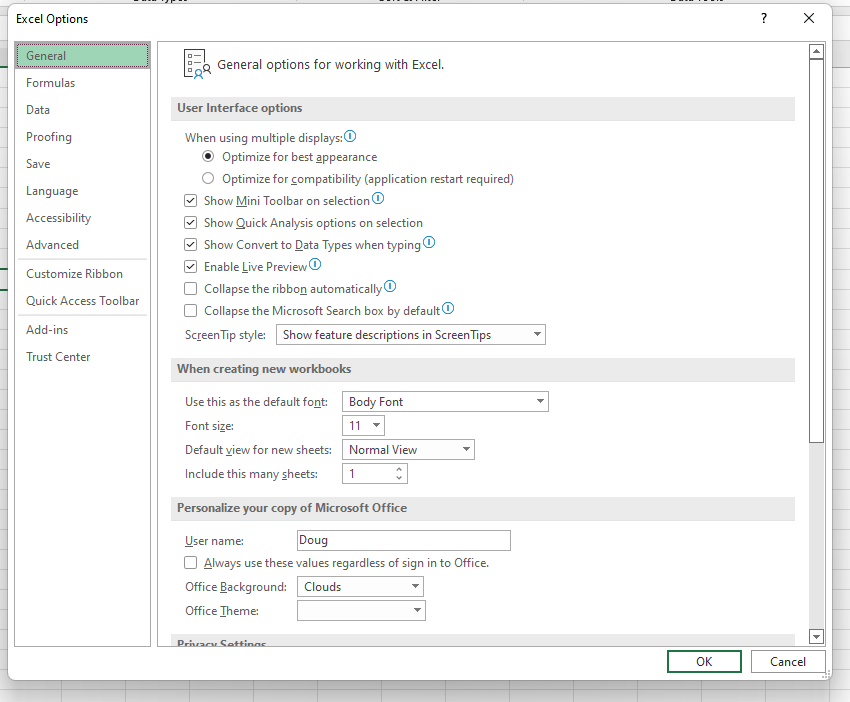
เลือก "Add-In" จากนั้นคลิกที่ "ไป"

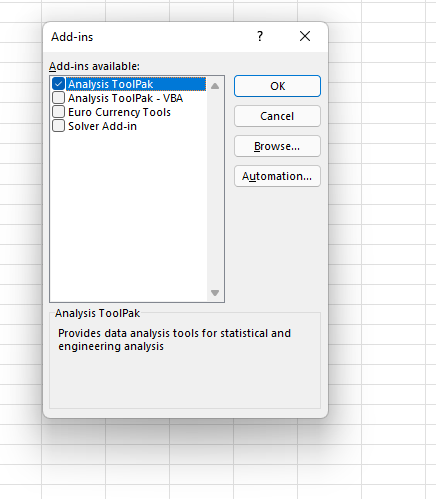
ตอนนี้ ให้ทำเครื่องหมายในช่องที่ระบุว่า "Analysis ToolPak" แล้วคลิก "ตกลง"

3. เลือก “ข้อมูล” จากเมนูแถบด้านบน

เมื่อคุณติดตั้ง ToolPak แล้ว ให้เลือก "ข้อมูล" จากเมนูแถบ Excel ด้านบน ซึ่งจะให้เมนูย่อยที่มีตัวเลือกการวิเคราะห์ที่หลากหลายสำหรับข้อมูลของคุณ

4. เลือก “การวิเคราะห์ข้อมูล” ที่มุมขวาบน

ตอนนี้ให้มองหา "การวิเคราะห์ข้อมูล" ที่มุมบนขวาแล้วคลิกเพื่อรับหน้าจอนี้:

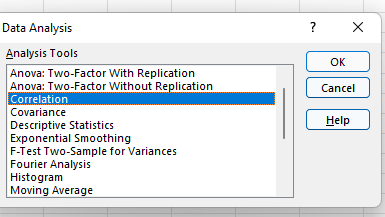
5. เลือก สหสัมพันธ์

เลือกความสัมพันธ์จากเมนูและคลิก "ตกลง"

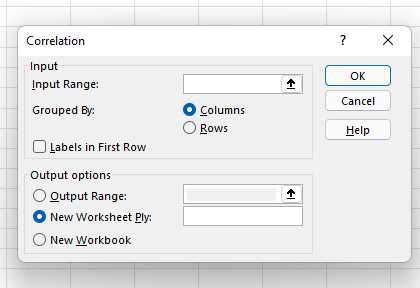
6. กำหนดช่วงข้อมูลและเอาต์พุตของคุณ

ตอนนี้กำหนดช่วงข้อมูลและเอาต์พุตของคุณ คุณเพียงแค่คลิกซ้ายแล้วลากเคอร์เซอร์ไปบนข้อมูลที่คุณต้องการเลือก จากนั้นระบบจะเติมข้อมูลอัตโนมัติในกล่องสหสัมพันธ์ สุดท้าย เลือกช่วงผลลัพธ์สำหรับข้อมูลความสัมพันธ์ของคุณ — เราเลือก A8 จากนั้นคลิก "ตกลง"

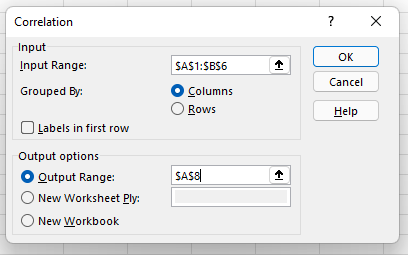
7. ประเมินค่าสัมประสิทธิ์สหสัมพันธ์ของคุณ

ผลลัพธ์ความสัมพันธ์ของคุณจะปรากฏขึ้น ในตัวอย่างของเรา ค่าในคอลัมน์ 1 และคอลัมน์ 2 มีความสัมพันธ์เชิงลบที่สมบูรณ์แบบ เมื่อตัวหนึ่งขึ้น อีกตัวหนึ่งลดลงในอัตราเดียวกัน

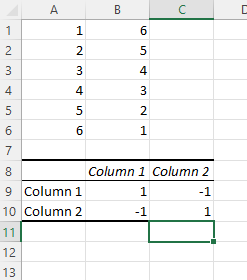
เมทริกซ์สหสัมพันธ์ของ Excel

ผลลัพธ์ความสัมพันธ์ของ Excel เรียกอีกอย่างว่าเมทริกซ์สหสัมพันธ์ของ Excel ในตัวอย่างข้างต้น ข้อมูลสองคอลัมน์ของเราสร้างเมทริกซ์การแก้ไขที่สมบูรณ์แบบที่ 1 และ -1 แต่จะเกิดอะไรขึ้นถ้าเราสร้างเมทริกซ์สหสัมพันธ์ที่มีชุดข้อมูลในอุดมคติน้อยกว่า

นี่คือข้อมูลของเรา:

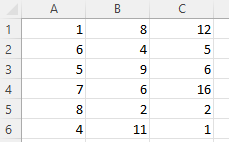
และนี่คือเมทริกซ์:

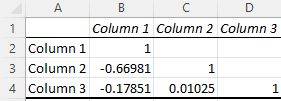
เซลล์ C4 ในเมทริกซ์ทำให้เรามีความสัมพันธ์ระหว่างคอลัมน์ 3 และคอลัมน์ 2 ซึ่งมีค่า 0.01025 ที่อ่อนแอมาก ในขณะที่คอลัมน์ 1 และคอลัมน์ 3 ให้ค่าความสัมพันธ์เชิงลบที่แข็งแกร่งกว่า -0.17851 อย่างไรก็ตาม ความสัมพันธ์ที่แข็งแกร่งที่สุดคือระหว่างคอลัมน์ 1 และคอลัมน์ 2 ที่ -0.66891

สิ่งนี้หมายความว่าอย่างไรในทางปฏิบัติ? สมมติว่าเรากำลังตรวจสอบผลกระทบของการกระทำที่เฉพาะเจาะจงต่อประสิทธิภาพของแคมเปญบนโซเชียลมีเดีย โดยที่คอลัมน์ 1 แสดงถึงจำนวนผู้เข้าชมที่คลิกผ่านโฆษณาบนโซเชียล และคอลัมน์ 2 และ 3 แสดงถึงแท็กไลน์ทางการตลาดที่แตกต่างกันสองแบบ เมทริกซ์สหสัมพันธ์แสดงความสัมพันธ์เชิงลบที่แข็งแกร่งระหว่างคอลัมน์ 1 และ 2 ซึ่งแสดงให้เห็นว่าแท็กไลน์เวอร์ชันคอลัมน์ 2 ลดการมีส่วนร่วมของผู้ใช้โดยรวมลงอย่างมาก ในขณะที่คอลัมน์ 3 ลดลงเพียงเล็กน้อยเท่านั้น

การสร้างเมทริกซ์ Excel เป็นประจำสามารถช่วยให้บริษัทต่างๆ เข้าใจผลกระทบของตัวแปรหนึ่งต่อตัวแปรอื่นได้ดีขึ้น และกำหนดว่า (ถ้ามี) ผลกระทบด้านลบหรือผลบวกใดที่อาจมีอยู่

สูตรสหสัมพันธ์ของ Excel

ถ้าคุณต้องการป้อนสูตรสหสัมพันธ์ด้วยตนเอง นั่นก็เป็นตัวเลือกเช่นกัน นี่คือสิ่งที่ดูเหมือน:

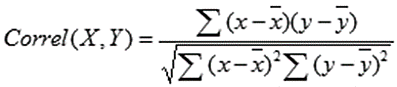
X และ Y คือค่าที่คุณวัด ∑ คือผลรวม และ X และ Y ที่มีแท่งขวางอยู่ด้านบนจะระบุค่าเฉลี่ยของค่าที่วัดได้ คุณจะคำนวณได้ดังนี้:

• คำนวณผลรวมของตัวแปร X ลบค่าเฉลี่ยของ X
• คำนวณผลรวมของตัวแปร Y ลบค่าเฉลี่ยของ Y
• คูณผลลัพธ์ทั้งสองนั้นและแยกตัวเลขนั้นออก (นี่คือผลลัพธ์แรก)
• ยกกำลังผลรวมของ X ลบค่าเฉลี่ยของ X. ยกกำลังผลรวมของ Y ลบด้วยค่าเฉลี่ยของ Y. คูณตัวเลขสองตัวนั้น
• หารากที่สอง (นี่คือผลลัพธ์ที่สอง)
• หารผลลัพธ์แรกด้วยผลลัพธ์ที่สอง
• คุณได้ค่าสัมประสิทธิ์สหสัมพันธ์

ง่ายใช่มั้ย? ใช่และไม่. แม้ว่าการใส่ตัวเลขจะไม่ซับซ้อน แต่ก็มักจะมีปัญหามากกว่าการสร้างและจัดการสูตรนี้ Excel Toolpak ในตัวมักจะเป็นวิธีที่ง่ายกว่า (และเร็วกว่า) ในการระบุค่าสัมประสิทธิ์และค้นหาความสัมพันธ์ที่สำคัญ

ความสัมพันธ์ ≠ ไม่ใช่สาเหตุ

ไม่มีบทความเกี่ยวกับความสัมพันธ์ที่สมบูรณ์โดยไม่ต้องพูดถึงว่าไม่เท่ากัน กล่าวอีกนัยหนึ่ง เพียงเพราะตัวแปรสองตัวขึ้นหรือลงพร้อมกัน ไม่ได้หมายความว่าตัวแปรหนึ่งเป็นสาเหตุของการเพิ่มขึ้นหรือลดลงของตัวแปรอีกตัวหนึ่ง

ขอ​พิจารณา​บาง​ตัว​อย่าง​ที่​แปลก​มาก.

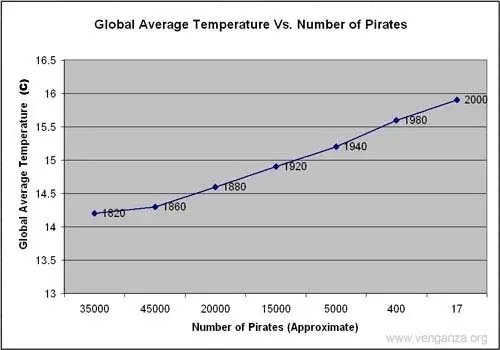
ภาพนี้แสดงให้เห็นความสัมพันธ์เชิงลบที่เกือบจะสมบูรณ์แบบระหว่างจำนวนโจรสลัดกับอุณหภูมิเฉลี่ยทั่วโลก — เนื่องจากโจรสลัดหายากขึ้น อุณหภูมิเฉลี่ยก็เพิ่มขึ้น

ปัญหา? แม้ว่าตัวแปรทั้งสองนี้จะสัมพันธ์กัน แต่ก็ไม่มีการเชื่อมโยงเชิงสาเหตุระหว่างทั้งสอง อุณหภูมิที่สูงขึ้นไม่ได้ลดจำนวนประชากรโจรสลัด และโจรสลัดน้อยลงไม่ได้ทำให้เกิดภาวะโลกร้อน

แม้ว่าสหสัมพันธ์เป็นเครื่องมือที่มีประสิทธิภาพ แต่ก็บ่งบอกถึงทิศทางของการเพิ่มขึ้นหรือลดลงระหว่างสองตัวแปรเท่านั้น ไม่ใช่สาเหตุของการเพิ่มขึ้นหรือลดลงนี้ ในการค้นหาสาเหตุเชื่อมโยง บริษัทต้องเพิ่มหรือลดตัวแปรหนึ่งตัวและสังเกตผลกระทบ ตัวอย่างเช่น หากความสัมพันธ์แสดงให้เห็นว่าการมีส่วนร่วมของลูกค้าเพิ่มขึ้นด้วยการใช้จ่ายบนโซเชียลมีเดีย ก็ควรเลือกใช้การใช้จ่ายที่เพิ่มขึ้นเล็กน้อยตามด้วยการวัดผลลัพธ์ หากการใช้จ่ายมากขึ้นนำไปสู่การมีส่วนร่วมที่เพิ่มขึ้นโดยตรง ลิงก์นั้นสัมพันธ์กันและเป็นเหตุเป็นผล หากไม่เป็นเช่นนั้น อาจมีปัจจัยหนึ่ง (หรือมากกว่า) ที่สนับสนุนการเพิ่มขึ้นของตัวแปรทั้งสอง

ให้ทันกับความสัมพันธ์

ความสัมพันธ์ของ Excel เป็นจุดเริ่มต้นที่มั่นคงสำหรับการพัฒนากลยุทธ์การตลาด การขาย และการใช้จ่าย แต่ไม่ได้บอกเล่าเรื่องราวทั้งหมด ด้วยเหตุนี้ จึงคุ้มค่าที่จะใช้ตัวเลือกการวิเคราะห์ข้อมูลในตัวของ Excel เพื่อประเมินความสัมพันธ์ระหว่างสองตัวแปรอย่างรวดเร็ว และใช้ข้อมูลนี้เป็นจุดเริ่มต้นสำหรับการวิเคราะห์เชิงลึกที่มากขึ้น