SVG Curves และ Bezier Curves: วิธีคำนวณ

เส้นโค้ง SVG เป็นเส้นโค้งเรียบต่อเนื่อง สามารถใช้เพื่อสร้างเส้น เส้นโค้ง ส่วนโค้ง และอื่นๆ สิ่งสำคัญที่สุดคือสามารถใช้เพื่อสร้าง เส้นโค้งเบซิเยร์ เส้นโค้งเบซิเยร์เป็นเส้นโค้งที่กำหนดโดยจุดสี่จุด จุดสองจุดแรกคือจุดเริ่มต้นและจุดสิ้นสุดของเส้นโค้ง และจุดสองจุดสุดท้ายคือจุดควบคุม จุดควบคุมกำหนดรูปร่างของเส้นโค้ง มีหลายวิธีในการคำนวณเส้นโค้งเบซิเยร์ วิธีที่พบมากที่สุดคือการใช้อัลกอริทึมของ De Casteljau อัลกอริทึมนี้ใช้ในการคำนวณคะแนนบนเส้นโค้งเบซิเยร์ อัลกอริทึมของ De Casteljau เป็นอัลกอริทึมแบบเรียกซ้ำ ซึ่งหมายความว่าจะแบ่งปัญหาออกเป็นปัญหาย่อยที่เล็กลง อัลกอริทึมเริ่มต้นด้วยจุดสี่จุดที่กำหนดเส้นโค้งเบซิเยร์ จากนั้นจะคำนวณจุดกึ่งกลางระหว่างจุดเริ่มต้นและจุดสิ้นสุด จุดกึ่งกลางนี้จะใช้ในการคำนวณจุดถัดไปบนเส้นโค้ง กระบวนการนี้ซ้ำจนกว่าจะถึงจำนวนคะแนนที่ต้องการ อัลกอริทึมของ De Casteljau ไม่ใช่วิธีเดียวในการคำนวณเส้นโค้งเบซิเยร์ มีวิธีอื่นเช่นการใช้ B-splines อย่างไรก็ตาม อัลกอริทึมของ De Casteljau เป็นวิธีที่พบได้บ่อยที่สุดและเป็นวิธีที่ใช้บ่อยที่สุด

นี่เป็นการติดตามโพสต์บล็อกก่อนหน้าของฉันเกี่ยวกับกราฟิกแบบเวกเตอร์ การจัดการและแอนิเมชั่นทำได้ง่ายด้วย SVG เพราะมีน้ำหนักเบา รวดเร็ว และเป็นธรรมชาติ เราจะกลับไปที่หัวข้อลำดับของเส้นและเส้นโค้งโดยใช้ภาพประกอบบางส่วน เดิมชื่อ เส้นโค้งเบซิเยร์ มาจากวิศวกรชาวฝรั่งเศสสองคนและได้รับการดัดแปลงอย่างเป็นทางการโดยพวกเขา พวกมันถูกจัดประเภทเป็นจุดควบคุมแบบสัมบูรณ์หรือแบบสัมพัทธ์ขึ้นอยู่กับบริบท เมื่อกดปุ่มเมาส์ กากบาทของเหตุการณ์ mouseDown จะปรากฏขึ้น และจุดที่ระบุว่าเส้นแนวนอนและแนวตั้งของเหตุการณ์ mouseDown ตัดกับเส้นโค้งบนหน้าจอ ตอนนี้จุดควบคุมสามารถแก้ไขได้ในโปรแกรมแก้ไขกราฟิกแบบเวกเตอร์ เช่น Illustrator ซึ่งกลายเป็นส่วนที่ใช้งานง่ายของประสบการณ์ผู้ใช้

การดำเนินการนี้ส่วนใหญ่เกิดขึ้นใน utilities/bezierIntersections.js สามารถมีรูทลูกบาศก์ได้มากถึงสามรูท และบางส่วนอาจเป็นพิกัดขยะสำหรับรูทที่ไม่อยู่ในสเป็คบนส่วนโค้งที่ประจบสอพลอ ในการหาจุดตัดของเส้นโค้งและเส้น เราใช้คำจำกัดความของเส้นโค้ง/เส้น เนื่องจากโค้ดเป็นการสาธิต ฉันไม่ได้ล้างพิกัดขยะ ฉันจดจ่ออยู่กับพีชคณิตแทนเพราะโค้ดเป็นเพียงการสาธิตเท่านั้น

ใช้สูตร (1-t)P0 + (t)P1 หากคุณต้องการหาจุด P ใดๆ บนเส้นตรง: P0 คือจุดเริ่มต้น และ P1 คือจุดสิ้นสุด

Bezier Curve คำนวณอย่างไร

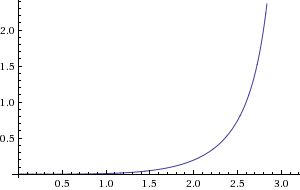
เส้นโค้งเบซิเยร์คำนวณโดยใช้สมการพาราเมตริกเพื่อกำหนดเส้นโค้ง สมการพาราเมตริกกำหนดพิกัด x และ y ของเส้นโค้งเป็นฟังก์ชันของพารามิเตอร์ t พารามิเตอร์ t สามารถเป็นจำนวนจริงใดๆ ระหว่าง 0 ถึง 1 เมื่อ t เป็น 0 พิกัด x และ y ของเส้นโค้งคือพิกัด x และ y ของจุดควบคุมแรก เมื่อ t เป็น 1 พิกัด x และ y ของเส้นโค้งคือพิกัด x และ y ของจุดควบคุมสุดท้าย สำหรับค่า t ระหว่าง 0 ถึง 1 พิกัด x และ y ของเส้นโค้งจะอยู่ระหว่างพิกัด x และ y ของจุดควบคุมจุดแรกและจุดสุดท้าย

คุณลักษณะที่ใช้บ่อยในคอมพิวเตอร์กราฟิกคือการใช้เส้นโค้งเอียง สามารถกำหนดได้ด้วยพหุนาม Bernstein (t = (1 – t))*n = 1 ใน Python เราสามารถคำนวณเส้นโค้งของช่วง[0, 1] เนื่องจากรูปร่างของเส้นโค้งถูกกำหนดโดย P1 ที่ 0 ต่อ 1 จึงสามารถเป็น 0 ต่อ 1 การคูณเมทริกซ์สามารถใช้แทนสูตรเบซิเยร์ได้ พหุนามแต่ละตัวเป็นฟังก์ชันของ Pis สองตัวในเมทริกซ์ โดยค่าสัมประสิทธิ์ของเมทริกซ์ทั้งหมดจะอยู่ตรงกลาง ด้วยวิธีนี้ เราสามารถตั้งโปรแกรมเวอร์ชันเส้นโค้งทั่วไปสำหรับจุดควบคุมจำนวนเท่าใดก็ได้โดยใช้ eq วาดเส้นโค้งเรียบโดยใช้ชุดของจุด

เมื่อเวกเตอร์สัมผัสถูกวาดด้วยจุดควบคุมที่ (x0, y0), (x1, y1), (x2, y2), (x3, y3) และ (x4, y4) แต่ละจุดบนเวกเตอร์สัมผัสจะเท่ากัน ทิศทาง. เส้นโค้ง Bezier เกิดจากส่วนนูนของจุด รูปสี่เหลี่ยมที่มีจุดยอดที่ (x0, y0), (x1, y1), (x2, y2) และ (x3, y3) เป็นผลมาจากเส้นโค้งพื้นที่สี่เหลี่ยมจัตุรัสที่มีจุดสี่จุด สมการต่อไปนี้ใช้เพื่อกำหนดตัวถังนูน รากที่สองของ * x0)2 เท่ากับรากที่สองของ * x0 (y) = b0)2. สำหรับ สมการเส้นโค้งเบซิเยร์ นี่คือสิ่งที่คุณควรทำ พูดอีกอย่างคือ =. มันเท่ากับ (x x0)2) (02) Y=0) คือชุดค่าผสมที่เหมาะสมที่สุด B0,3 เป็นหน่วยของ (1*u)3 ค่า =. รากที่สองของ (x x0)2 เท่ากับรากที่สองของ (x x0)2) (Y0) 2 คือสูตรสำหรับสิ่งนี้ (x x0)2) คือค่าที่แสดงถึงผลรวมของตัวเลขสองตัวที่อยู่ติดกัน เมื่อพูดถึง y (y y0) เราต้องใช้ (y y0) สำหรับ (x * x0)2) เท่ากับ (x * x0) = (x0 x1)2 + (y0 y1)2 = br>. 1,3=3u(1*u)2 เป็นหน่วยวัด B3,=3u2,(1*u) เป็นหน่วยการวัดประเภทหนึ่งในคณิตศาสตร์

เส้นทาง Svg ทำงานอย่างไร

เส้นทาง * สามารถวาดเส้น เส้นโค้ง ส่วนโค้ง และรูปทรงอื่นๆ เส้นทางอาจประกอบด้วยเส้นตรงหรือเส้นโค้งหลายๆ เส้น ทำให้เกิดรูปร่างที่ซับซ้อน รูปร่างที่ซับซ้อนที่ประกอบด้วยเส้นตรงเท่านั้นสามารถสร้างเป็น s ได้

ตัวเลขหรือตัวอักษรตัวเดียวใน เส้นทาง SVG อาจดูน่ากลัว อย่างไรก็ตาม มีจำนวนและตัวอักษรจำนวนมากในไฟล์ ในบทเรียนนี้ เราจะใช้เส้นทางเพื่อวาดสี่เหลี่ยมผืนผ้า และเราจะใช้เครื่องมือวาดภาพเพื่อทำสิ่งนี้ให้สำเร็จ Codepen หรือเครื่องมืออื่น ๆ ที่สามารถช่วยให้คุณเห็นได้อย่างรวดเร็วว่ามีการเปลี่ยนแปลงอะไรบ้างเป็นจุดเริ่มต้นที่ดีในการเขียนโค้ด แม้ว่าเราจะพยายามอย่างเต็มที่แล้ว แต่เราสามารถทำให้สิ่งต่างๆ ง่ายขึ้นสำหรับพวกเขาได้ ดังนั้น เมื่อวาดด้านขวาของสี่เหลี่ยมผืนผ้า เราต้องการให้ดินสออยู่บนแกน x ขณะที่เลื่อนขึ้น 200 บนแกน y เพิ่ม Y -200 ลงในสมการเพื่อเลื่อนขึ้น หลังจากนั้น เราสามารถใช้คำสั่ง z เพื่อคืนบรรทัดกลับสู่ตำแหน่งเดิม

เส้นทาง Svg และ Css

Mypath เป็นสัญลักษณ์ ความสูง:100px; width:115br> ความกว้าง 100px เท่ากับความกว้าง *br
svg path=”M10,L20″ *br Mypath %22br%22 หากต้องการแสดงภาพนี้ โปรดเปิดใช้ความสูง:100px โปรดดับเบิลคลิก *br> เพื่อแสดงความกว้างนี้ Mypath เป็นไดเร็กทอรีที่ใช้งานอยู่
พื้นหลัง: #FFF, *br*

Bezier Control Point คำนวณอย่างไร?

ไม่มีคำตอบที่ชัดเจนสำหรับคำถามนี้ เนื่องจากมีหลายวิธีที่สามารถคำนวณจุดควบคุมเบซิเยร์ขึ้นอยู่กับผลลัพธ์ที่ต้องการ วิธีการทั่วไปบางวิธีรวมถึงการใช้เส้นแบ่งครึ่งมุมของเส้นที่เชื่อมต่อจุดสิ้นสุดของเส้นโค้ง หรือการแก้ระบบสมการที่คำนึงถึงคุณสมบัติที่ต้องการของเส้นโค้ง อย่างไรก็ตาม โดยทั่วไปแล้ว จุดควบคุมจะถูกเลือกเพื่อสร้างเส้นโค้งเรียบที่ผ่านจุดสิ้นสุดที่กำหนด

ในการเขียนโปรแกรม เส้นโค้งเบซิเยร์เป็นคุณลักษณะที่รู้จักกันดี ใช้ในกราฟิกเพื่อสร้างกราฟิกแบบเวกเตอร์ที่ปรับขนาดได้ของเส้นโค้ง เพื่อให้แน่ใจว่าเส้นโค้งยังคงเรียบเสมอเมื่อเคลื่อนที่ผ่านเส้นโค้ง คุณต้องรู้สี่จุดในการวาด Bezier Curve: จุดเริ่มต้น จุดสิ้นสุด และจุดควบคุมสองจุด ระยะทางระหว่างจุดเริ่มต้นและจุดควบคุมขึ้นอยู่กับเส้นทางยาวเป็นเปอร์เซ็นต์ ใช้ในการคำนวณ Bezier Curve สำหรับจุดกึ่งกลางของสองจุด ให้คูณ M ด้วย P0 และ P1 ฉันไม่สามารถอธิบายได้เช่นเดียวกับวิดีโอ YouTube ดังนั้นโปรดดูหากคุณต้องการเรียนรู้เพิ่มเติม สูตรการหาค่าของจุด P ตาม Bezier Curve แสดงไว้ด้านล่าง

หน่วยวัดพื้นฐานสามหน่วยคือ P0 (จุด), P (จุดตามเส้น) และ T (เปอร์เซ็นต์ตามเส้น) P1 = (จุดสิ้นสุดที่ไม่รู้จัก) คือสูตรในการหาตัวเลขนี้ อัตราส่วนคือ 1 – p (t) – 0 / p

เวกเตอร์สัมผัสกับเส้นโค้งเบซิเยร์ที่จุดเริ่มต้น (จุดหยุด) ตั้งฉากกับเส้นที่เชื่อมระหว่างสองเส้นแรก (สองเส้นสุดท้าย) มีเวกเตอร์สัมผัสกับเส้นโค้ง Bezier ที่จุดเริ่มต้น (หยุด) แต่เส้นโค้งเอียงไปทางขวา เป็นไปไม่ได้ที่จะสร้าง Bezier curve ด้วยตนเองด้วยอัลกอริทึมแบบเรียกซ้ำ ระบบจะเริ่มต้นด้วยจุดควบคุมแรกและสิ้นสุดด้วยเส้นโค้งที่เดินทางผ่านจุดควบคุมถัดไป มันใช้งานง่าย แต่ก็สามารถใช้เพื่อสร้างเส้นโค้งของคำสั่งใดก็ได้ โดยทั่วไป เส้นโค้งจะเริ่มต้นที่จุดควบคุมจุดแรก ที่จุดที่สอง เส้นโค้งจะตัดแกน y สุดท้าย เส้นโค้งตัดแกน x ที่จุดที่สาม จุดควบคุมที่สี่อยู่ที่จุดที่เส้นโค้งตัดกับเส้นที่เชื่อมต่อจุดควบคุมสองจุดแรก จุดควบคุมที่ห้าคือจุดที่เส้นโค้งตัดกับเส้นที่เชื่อมต่อจุดควบคุมที่สองและสาม จุดควบคุมที่หกเชื่อมต่อจุดควบคุมที่สามและสี่เนื่องจากเป็นจุดที่เส้นโค้งตัดกับเส้น จุดควบคุมที่เจ็ดคือจุดที่เส้นโค้งตัดกับเส้นที่เชื่อมระหว่างจุดควบคุมที่สี่และห้า จุดควบคุมที่แปดคือจุดที่เส้นโค้งตัดกับเส้นที่เชื่อมต่อจุดควบคุมที่ห้าและหก จุดควบคุมที่เก้าคือจุดที่เส้นโค้งตัดกับเส้นที่เชื่อมต่อจุดควบคุมที่หกและเจ็ด เมื่อเส้นโค้งตัดกับเส้นที่เชื่อมต่อจุดควบคุมที่เจ็ดและแปด จุดควบคุมที่สิบจะถูกกำหนด จุดควบคุมอยู่ที่จุดควบคุมที่สิบเอ็ดและเก้าตามลำดับ ณ จุดที่เส้นโค้งตัดกับเส้นที่เชื่อมต่อจุดควบคุมที่แปดและเก้า จุดควบคุมที่สิบสองคือจุดที่เส้นโค้งตัดกับเส้นที่เชื่อมต่อจุดควบคุมที่เก้าและสิบ เส้นโค้งสามารถวาดในลำดับใดก็ได้ แต่ไม่ใช่ทุกจุดที่มีประโยชน์ในทางปฏิบัติ จุดที่จุดเริ่มต้นและจุดสิ้นสุดของเส้นโค้งมักจะมีประโยชน์มากที่สุด แต่ก็อาจมีประโยชน์ที่จุดกึ่งกลางของเส้นโค้งได้เช่นกัน อัลกอริทึม Bezier Curve นั้นตรงไปตรงมา แต่คุณสามารถใช้เพื่อสร้างรูปร่างใดๆ ก็ได้

คุณวาดเส้นโค้งใน Svg ได้อย่างไร?

ในการวาดเส้นโค้งใน svg คุณต้องสร้างองค์ประกอบและกำหนดแอตทริบิวต์โฆษณาบนองค์ประกอบนั้น d แอตทริบิวต์กำหนดเส้นทางข้อมูลสำหรับองค์ประกอบ ข้อมูลเส้นทางประกอบด้วยชุดคำสั่งและพารามิเตอร์ แต่ละคำสั่งประกอบด้วยตัวอักษรและตัวเลข ตัวอักษรแสดงถึงคำสั่งและตัวเลขแสดงถึงพารามิเตอร์ คำสั่งสำหรับการวาดเส้นโค้ง ได้แก่ C, c, S, s, Q, q, T, t, A, a คำสั่ง C ย่อมาจาก "เส้นโค้งเบซิเยร์ลูกบาศก์สัมบูรณ์" คำสั่ง c ย่อมาจาก "relative cubic Bezier curve" คำสั่ง S ย่อมาจาก "เส้นโค้งเบซิเยร์ลูกบาศก์เรียบสัมบูรณ์" คำสั่ง s หมายถึง "เส้นโค้ง Bezier ลูกบาศก์เรียบสัมพัทธ์" คำสั่ง Q ย่อมาจาก "เส้นโค้ง Bezier กำลังสองสัมบูรณ์" คำสั่ง q หมายถึง “เส้นโค้ง Bezier กำลังสองสัมพัทธ์” คำสั่ง T ย่อมาจาก “Absolute Smooth Quadratic Bezier Curve” คำสั่ง t หมายถึง "เส้นโค้ง Bezier กำลังสองสัมพัทธ์แบบเรียบ" คำสั่ง A ย่อมาจาก "ส่วนโค้งวงรีสัมบูรณ์" คำสั่ง a หมายถึง "ส่วนโค้งวงรีสัมพัทธ์" แต่ละคำสั่งเหล่านี้มีชุดพารามิเตอร์ที่แตกต่างกันซึ่งกำหนดเส้นโค้ง

คำสั่งเส้นโค้งลูกบาศก์เบซิเยร์ (C) จะเป็นดังนี้: [code type=html] มันคือ =1, =1, =1, =1, =1, =1, =1, =1, =1, =1, =1, =1, =1, =1 เส้นโค้งเริ่มต้นที่จุด 100,200 ที่ซึ่งเส้นทางดำเนินไป จุดควบคุมที่สองคือ 400,100 เส้นโค้งมีค่า 400,200 ที่ส่วนท้าย เส้นโค้ง เช่น เส้น ไม่จำเป็นต้องโค้งอย่างต่อเนื่อง หากคุณเชื่อมต่อเส้นโค้งหนึ่งเข้ากับอีกเส้นโค้งหนึ่ง คุณสามารถสร้างเส้นโค้งที่ซับซ้อนยิ่งขึ้นได้ คำสั่งเหล่านี้หรือที่เรียกว่า S และ S ถูกใช้โดยเบราว์เซอร์เพื่อให้คุณค้นหาสิ่งที่ต้องการได้ง่ายขึ้น

เวลานี้ เส้นโค้งสองเส้นจะแสดงโดยใช้ทางลัดสัมบูรณ์ ในการทำงานกับ เบซิเยร์กำลังสอง จำเป็นต้องมีจุดควบคุมหนึ่งจุดแทนที่จะเป็นสองจุด ด้วยคำสั่ง arc พารามิเตอร์ส่วนใหญ่จะถูกพิจารณา คำสั่งเส้นโค้งมีสามประเภท จุดเริ่มต้นและจุดสิ้นสุด วงรีที่มีการหมุนแกน rx, ry และ x และส่วนโค้งทั้งสี่เป็นไปได้ทั้งหมด ส่วนโค้งใช้เพื่อสะท้อนภาพธงส่วนโค้งขนาดใหญ่ในภาพธงกวาด ส่วนโค้งสีน้ำเงินแสดงถึงส่วนโค้งสีแดงที่ก่อตัวรอบแกนเมื่อปลายทั้งสองชี้ไปในทิศทางเดียวกัน

ดังนั้น ค่า 0 บ่งชี้ว่าควรใช้ส่วนโค้งที่เล็กกว่า ขณะที่ค่า 1 ระบุว่าควรใช้ส่วนโค้งที่ใหญ่กว่า เส้นทางมีขนาดใหญ่และมีประสิทธิภาพมากกว่ารูปทรงพื้นฐาน สามารถสร้างขึ้นได้โดยใช้ความพยายามเพียงเล็กน้อย แต่ไม่มากนัก คุณมีโอกาสที่ดีที่โปรแกรมแก้ไขกราฟิกทั้งหมดจะส่งออกรูปภาพเป็นเส้นทาง เป็นการดีที่สุดที่จะจดจำคำสั่งในเวลาไม่กี่นาที

เรียนรู้วิธีสร้างเส้นทางใน Svg

เมื่อใช้เส้นทางใน SVG คุณสามารถสร้างรูปทรงต่างๆ รวมถึงวงกลมและเส้นโค้งได้ ในบทความนี้ เราจะดูวิธีใช้คำสั่งเหล่านี้เพื่อสร้างเส้นทางเหล่านี้
สามารถใช้คำสั่ง A เพื่อสร้างส่วนโค้งใน SVG หลังจากเปิดหน้าต่างคำสั่ง arc แล้ว คุณจะสามารถระบุรัศมี x และ y ของวงกลมหรือวงรีที่จะใช้สร้างส่วนโค้งได้ คุณยังสามารถรวมจุดเริ่มต้นและจุดสิ้นสุดของส่วนโค้ง ตลอดจนมุมที่ควรวาด
คำสั่ง C ช่วยให้คุณสร้างเส้นทางโค้งได้เช่นกัน หากคุณใช้ มันจะระบุเส้นทางที่ต้องวาด เช่นเดียวกับสัญลักษณ์องค์ประกอบและสัญลักษณ์ที่ขาดหายไป คำนิยามพาธคือรายการของคำสั่งพาธ ซึ่งแต่ละคำสั่งจะแสดงด้วยตัวอักษรคำสั่งและตัวเลขที่แสดงถึงพารามิเตอร์
ตัวอย่างเช่น หากต้องการให้พาธอยู่กึ่งกลางใน SVG คุณสามารถใช้แอตทริบิวต์ viewBox โดยจะจัดเส้นทางให้อยู่กึ่งกลางในวิวพอร์ตโดยไม่คำนึงว่าพบตำแหน่งใดในเอกสาร

เครื่องสร้าง Svg Bezier Curve

มีเครื่องกำเนิดเส้นโค้ง svg bezier จำนวนมากทางออนไลน์ ตัวสร้างเหล่านี้ช่วยให้คุณสร้าง เส้นโค้ง bezier svg ที่กำหนดเอง ตามพารามิเตอร์ที่คุณระบุ คุณสามารถควบคุมความกว้าง ความสูง จำนวนจุดควบคุม และลักษณะอื่นๆ ของเส้นโค้งได้ เครื่องมือสร้างเหล่านี้เป็นวิธีที่ยอดเยี่ยมในการสร้างรูปร่างและการออกแบบที่กำหนดเองสำหรับโครงการเว็บของคุณ

เส้นโค้งเส้นทาง Svg

SVG Path Curves ใช้เพื่อสร้างเส้นโค้งเรียบบนเส้นทาง SVG เส้นโค้งมีสี่ประเภท: เส้นโค้งกำลังสอง เส้นโค้งลูกบาศก์ เส้นโค้งส่วนโค้ง และเส้นโค้งเรียบ เส้นโค้งแต่ละประเภทมีข้อดีและข้อเสียต่างกันไป ดังนั้นการเลือกประเภทของเส้นโค้งให้เหมาะสมกับงานจึงเป็นเรื่องสำคัญ เส้นโค้งกำลังสองเป็นเส้นโค้งประเภทที่ง่ายที่สุดและสร้างและจัดการได้ง่าย เส้นโค้งลูกบาศก์นั้นซับซ้อนกว่าและสามารถใช้สร้างรูปทรงที่มีรายละเอียดมากขึ้นได้ เส้นโค้งส่วนโค้งเหมาะที่สุดสำหรับการสร้างรูปทรงกลมหรือวงรี เส้นโค้งเรียบคือการรวมกันของเส้นโค้งอีกสามประเภท และสามารถใช้เพื่อสร้างรูปทรงต่างๆ ได้

เส้นทางคือรูปทรงเรขาคณิตของโครงร่างของวัตถุที่กำหนดโดยการย้ายรูปร่างของวัตถุไปด้านหนึ่ง lineto, curveto (ทั้งความชันแบบลูกบาศก์และกำลังสอง), ส่วนโค้ง และเส้นทางระยะใกล้ เส้นทางผสม (เช่น เส้นทางที่มีเส้นทางย่อยหลายเส้นทาง) สามารถใช้เพื่อให้วัตถุมีรูโดนัทได้ โดยจะอธิบายถึงไวยากรณ์ ลักษณะการทำงาน และอินเทอร์เฟซ DOM ของ เส้นทาง SVG และวิธีการแสดงออก แต่ละคำสั่งในลำดับข้อมูลพาธตามด้วยอักขระตัวเดียว ไวยากรณ์ของข้อมูลพาธมีความกระชับเพื่อให้มีขนาดไฟล์ที่เล็กที่สุด ในขณะเดียวกันก็ช่วยให้ดาวน์โหลดได้อย่างมีประสิทธิภาพ ข้อมูลพาธสามารถแบ่งออกเป็นหลายบรรทัดเพื่อปรับปรุงการอ่าน เนื่องจากอักขระในนั้นประกอบด้วยอักขระขึ้นบรรทัดใหม่ ด้วยการใช้ประโยชน์จากอักขระช่องว่างที่ทำให้เป็นมาตรฐานในมาร์กอัป บรรทัดใหม่ในชื่อแอตทริบิวต์จะถูกทำให้เป็นมาตรฐาน

ค่านี้แสดงถึงรูปร่างที่สตริงข้อมูลพาธระบุ ข้อผิดพลาดภายในสตริงจะได้รับการจัดการตามส่วนการจัดการข้อผิดพลาดข้อมูลเส้นทางของข้อมูลเส้นทาง กลุ่มข้อมูลเส้นทาง (ถ้ามี) ต้องขึ้นต้นด้วยคำสั่ง moveto (ถ้ามี) เส้นตรงจะถูกลากจากจุดปัจจุบันไปยังจุดเริ่มต้นของเส้นทางย่อยปัจจุบันโดยอัตโนมัติ เป็นไปได้ว่าส่วนของเส้นทางนี้ไม่มีความยาวเลย Closepath ถูกกำหนดให้เป็นเส้นทางที่เข้าร่วมโดยจุดเริ่มต้นของเซ็กเมนต์เริ่มต้นโดยใช้ค่า 'เส้นขีดเส้นร่วม' ที่ส่วนท้ายของเซ็กเมนต์สุดท้าย เมื่อส่วนพาธแรกและพาธสุดท้ายไม่ถูกเชื่อม จะมีความแตกต่างระหว่างพาธย่อยแบบปิดและพาธย่อยแบบเปิด

ปัจจุบัน Python ไม่สนับสนุนการดำเนินการปิดพาธแบบเซ็กเมนต์ที่สมบูรณ์เป็นคำสั่ง ในการเปลี่ยนจุดอ้างอิง บรรทัดคำสั่งอาจลากเส้นตรงจากจุดหนึ่งไปยังอีกจุดหนึ่ง เมื่อใช้คำสั่งสัมพัทธ์ l เพื่อสร้างบรรทัด จุดสิ้นสุดคือ (cpy x) ในการวาดเส้นแนวนอนในทิศทางของแกน x ที่เป็นบวก ให้ใช้คำสั่ง h สัมพัทธ์ที่มีค่า x เป็นบวก ห้าตัวอย่างแรกแสดงให้เห็นส่วนลูกบาศก์เดียวของ เส้นทาง Bezier จากมากไปน้อย คุณสามารถสั่งส่วนโค้งวงรีได้ หากคุณใช้คำสั่งสัมพัทธ์ ส่วนโค้งจะแสดงด้วยพิกัด (cxy)

ธงขนาดใหญ่และกวาดระบุจำนวนของส่วนโค้งที่วาด ดังแสดงในแผนภาพด้านล่าง การประมวลผล EBNF ต้องใช้การผลิตที่กำหนดมากที่สุดเท่าที่จะเป็นไปได้ เพื่อที่จะหยุด ณ จุดที่ตัวละครไม่เป็นไปตามข้อกำหนดสำหรับการผลิตนั้นอีกต่อไป เมื่อค่าของคุณสมบัติ d เป็นศูนย์ การเรนเดอร์จะถูกปิดใช้งาน เมื่อคำนวณรูปร่างแคปและแสดงเครื่องหมายที่ขอบเขตเซ็กเมนต์ การแทนที่จะถูกเปิดใช้งานสำหรับขอบเขตเซ็กเมนต์ ถ้าทั้ง rx และ ry เป็นศูนย์ ส่วนโค้งนี้จะถือว่าเป็นส่วนของเส้นตรง (เส้นที่เชื่อมต่อจุดสิ้นสุด) สำหรับข้อมูลเพิ่มเติมเกี่ยวกับการดำเนินการมาตราส่วนนี้ ดูส่วนภาคผนวกสำหรับสูตรทางคณิตศาสตร์ ส่วนเส้นทางที่มีความยาวเป็นศูนย์นั้นไม่ถูกต้อง และจะส่งผลต่อการแสดงผลในกรณีต่อไปนี้

การเพิ่มแอตทริบิวต์ 'pathLength' ให้กับเส้นทาง ผู้เขียนสามารถคำนวณความยาวทั้งหมดของเส้นทาง เพื่อให้ตัวแทนผู้ใช้สามารถคำนวณระยะทางตามเส้นทางได้ การดำเนินการเคลื่อนที่ภายในองค์ประกอบ 'เส้นทาง' สามารถพิจารณาการดำเนินการที่มีความยาวเป็นศูนย์ สามารถใช้เส้น เส้นโค้ง และลูกศรเพียงไม่กี่เส้นในการคำนวณความยาวของเส้นทาง

เส้นทาง เส้นโค้ง และส่วนโค้ง: พื้นฐานขององค์ประกอบเส้นทาง

โดยทั่วไปแล้วเส้นทางจะถูกกำหนดโดยใช้องค์ประกอบ 'เส้น' และสามารถสร้างเส้นตรงได้ นอกจากนี้ยังสามารถใช้องค์ประกอบ 'เส้นโค้ง' เพื่อเติมเส้นโค้งด้วยองค์ประกอบ 'เติม' หรือ 'เส้นขีด'
หากคุณต้องการสร้างเส้นทางที่ผ่านจุดต่างๆ สองสามจุด คุณสามารถใช้องค์ประกอบ 'ส่วนโค้ง' องค์ประกอบ 'ส่วนโค้ง' มีสองลักษณะ: จุดเริ่มต้นและจุดสิ้นสุด ขนาดของส่วนโค้งสามารถระบุได้โดยการระบุรัศมี
สุดท้าย รูปทรงสามารถใช้เพื่อสร้างเส้นทางได้ มีสององค์ประกอบในองค์ประกอบ 'เส้นทาง': จุดเริ่มต้นและจุดสิ้นสุด แอตทริบิวต์องศาหรือที่เรียกว่าองค์ประกอบโฆษณารวมเป็นส่วนหนึ่งขององค์ประกอบเส้นทาง ระดับการเคลื่อนที่ของเส้นทางรอบรูปร่างระบุไว้ที่นี่
ด้วยเหตุนี้ จึงมีหลายวิธีในการใช้เส้นทาง และส่วนประกอบทั้งหมดจะสรุปไว้ในองค์ประกอบ 'เส้นทาง' เนื่องจากองค์ประกอบเส้นทางมีแอตทริบิวต์เดียว แอตทริบิวต์ 'd' ซึ่งบอกว่าจะวาดรูปร่างใด โปรดอย่าลืมว่าองค์ประกอบนั้นประกอบด้วยแอตทริบิวต์เดียว

ตัวอย่างเส้นทาง Svg

เส้นทาง SVG กำหนดรูปร่างของวัตถุเป็นชุดของเส้นและเส้นโค้งที่เชื่อมต่อกัน ตัวอย่างเส้นทาง svg กำหนดรูปร่างของหัวใจ

องค์ประกอบเส้นทางเป็นองค์ประกอบสุดท้ายในภาพวาด จำเป็นต้องมีแอตทริบิวต์ d เพื่ออธิบายสิ่งที่วาด มีฟังก์ชั่นมากมายในนั้น แต่ส่วนใหญ่เป็นเพียงไวยากรณ์ขนาดเล็กที่มีค่าที่อ่านไม่ออกซึ่งมองเห็นได้ง่าย เราสามารถจัดรูปแบบรหัสใหม่เพื่อให้เข้าใจได้ (ยังคงมีอักขระเดิมอยู่) เส้นทางสามารถใช้เพื่อวาดเส้นตรงกลับไปยังจุดที่ตั้งปากกาได้ ทำให้เป็นวิธีที่ประหยัดและง่าย เส้นทางต้องปิดด้วย Z (หรือ z ไม่สำคัญ) เช่นเดียวกับคำสั่งอื่นๆ และเป็นคำสั่งเผื่อเลือก คำสั่ง A เป็นสิ่งที่ยากที่สุด ในการกำหนดความกว้าง ความสูง และการหมุนของวงรี คุณต้องระบุเส้นทางที่คาดว่าจะใช้ มีสองวงรีที่เป็นไปได้สำหรับเส้นทางที่จะเดินทางไปรอบๆ สองเส้นทางที่แตกต่างกันสำหรับแต่ละวงรี และสี่เส้นทางที่แตกต่างกันสำหรับแต่ละวงรี

ลูกบาศก์เบซิเยร์

เส้นโค้งเบซิเยร์ลูกบาศก์เป็นเส้นโค้งพาราเมตริกที่ใช้บ่อยในคอมพิวเตอร์กราฟิกส์และสาขาที่เกี่ยวข้อง เส้นโค้งถูกกำหนดโดยจุดสี่จุด: จุดสิ้นสุดสองจุดและจุดควบคุมสองจุด เส้นโค้ง Bezier สามารถรวมกันเพื่อสร้าง Bezier spline ซึ่งเป็นเส้นโค้งที่กำหนดเป็นชิ้นส่วนซึ่งประกอบด้วยเส้นโค้ง Bezier หลายเส้นที่เชื่อมต่อกันตั้งแต่ต้นจนจบ

ทำความเข้าใจคณิตศาสตร์เบื้องหลังเส้นโค้งเบซิเยร์และความเกี่ยวข้องของฟังก์ชันจับเวลาอื่นๆ ในวิดีโอนี้ คุณสามารถปรับแต่งการแสดงภาพของคุณเพื่อสะท้อนคณิตศาสตร์ที่อยู่เบื้องหลังการเปลี่ยนผ่านที่สวยงามเหล่านี้ได้โดยใช้การแสดงภาพแบบโต้ตอบ เส้นโค้งเป็นเส้นโค้งชนิดพิเศษที่สามารถใช้เพื่ออธิบายกระบวนการเคลื่อนที่จากสถานะหนึ่งไปยังอีกสถานะหนึ่ง ตอนนี้เราสามารถย้ายอย่างต่อเนื่องระหว่างส่วนบนแกน P0 -> P1 รวมทั้ง P1 -> P2 เส้นทางที่คล้ายกับ เส้นโค้ง Bezier กำลังสอง สามารถรับได้หากเราเชื่อมโยงจุดทั้งสองนี้กับส่วนและวางตำแหน่งจุดแก้ไข (จุดสีน้ำเงิน) บนนั้น เป็นที่รู้จักกันว่าการแก้ไขเชิงเส้น เริ่มต้นด้วยจุดควบคุม P0, P1, P2 และ P3 เราจะใช้สูตรเพื่อแสดงเส้นโค้งเบซิเยร์ลูกบาศก์

เมื่อเราเพิ่มจุดที่สี่ – P4 – ในแต่ละส่วนที่เชื่อมโยงจุดทั้งสี่ เราจะได้จุดที่สอดแทรกระหว่างส่วน ด้วยเหตุนี้ เราจึงเชื่อมโยงจุดเหล่านี้และสร้างจุด (*) ที่สอดแทรก (*) สำหรับแต่ละส่วนใหม่ (สีเขียว) ขั้นตอนต่อไปคือการเชื่อมโยงจุดและวาดส่วนของแต่ละจุด ในที่สุดเราก็มีสูตรสำหรับการวาดเส้นโค้ง ต่อไปนี้เป็นวิธีแสดงสูตรคิวบ์เบซิเยร์ ( P0, P1, P2, P3) = สำหรับ (ให้ t = 0, t = 1 <= 1); t = 1 กล่าวอีกนัยหนึ่ง สมการนี้มี 1 ต่อ 60 res

กด ( x: valX, y: valY ); ความละเอียด พิกัด P1 และ P2 แสดงถึงการเคลื่อนที่ขององค์ประกอบ และเมื่อมันเปลี่ยนผ่าน ก็จะเป็นไปตามเส้นโค้งนี้ นี่คือวิธีที่แนวคิดทางคณิตศาสตร์เปลี่ยนเป็นการเคลื่อนไหว การใช้เส้นโค้งเฉพาะกับการเปลี่ยนคิวบ์เบซิเยร์ที่เฉพาะเจาะจงสามารถใช้เพื่อแสดงถึงการเปลี่ยนผ่านแบบง่ายที่หลากหลาย เพื่อความสะดวก CSS จัดเตรียมฟังก์ชันการจับเวลาเหล่านี้ทั้งหมด Framer Motion พบว่ามีความสัมพันธ์ที่แน่นแฟ้นระหว่างฟังก์ชันการค่อยๆ เปลี่ยนและการย้ายข้อมูลในออบเจกต์การเปลี่ยนภาพ ฟังก์ชันลูกบาศก์เบซิเยร์ ใน Framing Motion แตกต่างจากที่เราเคยเห็นใน CSS อย่างมาก

ค่าของคะแนน P1 และ P2 ตามลำดับ จะต้องส่งผ่านไปยังคุณสมบัติความง่ายเพื่ออธิบายการเปลี่ยนแปลงนี้ บล็อกโพสต์นี้ให้ข้อมูลเชิงลึกที่น่าสนใจเกี่ยวกับของเจ๋งๆ บางอย่างที่เราใช้ในชีวิตประจำวัน และฉันหวังว่าคุณจะสนใจ ด้วยความรู้เพิ่มเติมเกี่ยวกับ ฟังก์ชันลูกบาศก์เบซิเยร์ และคำแนะนำ คุณจะสามารถสร้างทรานซิชันและแอนิเมชันใหม่ได้อย่างง่ายดาย