SVG 曲線和貝塞爾曲線：如何計算它們

SVG 曲線是連續的平滑曲線。 它可用於創建直線、曲線、圓弧等。 最重要的是，它可以用來創建貝塞爾曲線。 貝塞爾曲線是由四個點定義的曲線。 前兩點是曲線的起點和終點，後兩點是控制點。 控制點決定曲線的形狀。 有很多方法可以計算貝塞爾曲線。 最常見的方法是使用 De Casteljau 算法。 該算法用於計算貝塞爾曲線上的點。 De Casteljau 算法是一種遞歸算法。 這意味著它將問題分解為更小的子問題。 該算法從定義貝塞爾曲線的四個點開始。 然後計算起點和終點之間的中點。 然後使用該中點計算曲線上的下一個點。 重複此過程，直到達到所需的點數。 De Casteljau 算法並不是計算貝塞爾曲線的唯一方法。 還有其他方法，例如使用 B 樣條。 然而，De Casteljau 算法是最常見的方法，也是使用最頻繁的一種方法。

這是我之前關於矢量圖形的博文的後續。 使用 SVG 可以輕鬆地進行操作和動畫製作，因為它們輕巧、快速且自然。 我們將藉助一些插圖回到直線和曲線序列的主題。 貝塞爾曲線最初以兩位法國工程師的名字命名，並由他們正式改編。 根據上下文，它們被分類為絕對或相對控制點。 按下鼠標按鈕時，會顯示 mouseDown 事件的十字線，點表示 mouseDown 事件的水平線和垂直線與屏幕上的曲線相交的位置。 現在可以在 Illustrator 等矢量圖形編輯器中編輯控制點，這已成為用戶體驗的直觀組成部分。

此操作主要發生在 utilities/bezierIntersections.js 中。 可以有多達三個立方根，其中一些可能是較平坦曲線段上超出規格根的垃圾坐標。 為了找到曲線和直線的交點，我們使用曲線/直線的定義。 因為代碼是demo，我沒有清理垃圾坐標； 相反，我專注於代數，因為代碼只是一個演示。

如果要沿直線找到任意點 P，請使用公式 (1-t)P0 + (t)P1：P0 是起點，P1 是終點。

貝塞爾曲線是如何計算的？

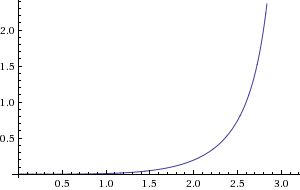
貝塞爾曲線是通過使用參數方程來定義曲線來計算的。 參數方程將曲線的 x 和 y 坐標定義為參數 t 的函數。 參數t可以是0到1之間的任意實數。當t為0時，曲線的x、y坐標為第一個控制點的x、y坐標。 當t為1時，曲線的x、y坐標為最後一個控制點的x、y坐標。 對於介於 0 和 1 之間的 t 值，曲線的 x 和 y 坐標介於第一個和最後一個控制點的 x 和 y 坐標之間。

計算機圖形學中經常使用的功能是使用斜角曲線。 它們可以由伯恩斯坦多項式 (t = (1 – t))*n = 1 來定義。在 Python 中，我們可以計算範圍 [0, 1] 的曲線。 因為曲線的形狀完全由0到1的P1決定，所以可以是0到1。可以用矩陣乘法來表示貝塞爾公式。 每個多項式都是矩陣中兩個Pi的函數，矩陣的係數都以它們為中心。 以這種方式，我們可以使用等式為任意數量的控制點編程通用曲線版本。 借助一組點繪製平滑曲線。

當控制點位於 (x0, y0)、(x1, y1)、(x2, y2)、(x3, y3) 和 (x4, y4) 處繪製切向量時，切向量上的每個點具有相同的方向。 貝塞爾曲線由點的凸包形成。 頂點位於 (x0, y0)、(x1, y1)、(x2, y2) 和 (x3, y3) 的四邊形是具有四個點的求積曲線的結果。 以下等式用於定義凸包。 * x0)2 的平方根等於 * x0 的平方根。 (y) = b0)2。 對於貝塞爾曲線方程，這是您應該做的。 換句話說，=。 它等於 (x x0)2)。 (02) Y=0) 是最合適的組合。 B0,3是(1*u)3的單位。 價值=。 (x x0)2 的平方根等於 (x x0).2) 的平方根。 (Y0) 2 就是這個的公式。 (x x0)2) 是表示兩個相鄰數字之和的值。 說到y(y y0)，就要用(y y0)。 因為 (x * x0)2) 等於 (x * x0)。 = (x0 x1)2 + (y0 y1)2 = br>。 1,3=3u(1*u)2是計量單位。 B3,=3u2,(1*u)是數學中的一種計量單位。

Svg 路徑如何工作？

*path 可以繪製直線、曲線、圓弧等形狀。 路徑可以由多條直線或曲線組成，從而產生復雜的形狀。 僅由直線組成的複雜形狀可以生成為 s。

SVG 路徑中的單個數字或字母可能顯得令人生畏； 但是，文件中有很多數字和字母。 在本課中，我們將使用路徑繪製矩形，並使用繪圖工具來完成此操作。 Codepen 或任何其他可以讓您快速查看正在進行的更改的工具是開始編碼的好地方。 儘管我們盡了最大努力，但我們可以讓他們的事情變得更容易。 因此，在繪製矩形的右側時，我們希望鉛筆保持在 x 軸上，同時在 y 軸上向上移動 200。 將 Y -200 添加到等式中以向上移動。 之後，我們可以使用 z 命令將一行返回到其原始位置。

Svg 路徑和 Css

我的路徑是一個符號。 高度：100px； width:115br> 100px 的寬度等於 *br 的寬度。
svg path=”M10,L20″ *br Mypath %22br%22 要顯示此圖像，請啟用高度：100px。 請雙擊 *br> 以顯示此寬度。 Mypath 是一個活動目錄。
背景：#FFF，*br*。

貝塞爾曲線控制點是如何計算的？

這個問題沒有一個明確的答案，因為有多種方法可以根據所需的結果計算貝塞爾曲線控制點。 一些常見的方法包括使用連接曲線端點的直線的角平分線，或者通過求解考慮曲線所需特性的方程組。 然而，一般來說，通常選擇控制點，以便它們創建通過給定端點的平滑曲線。

在編程中，貝塞爾曲線是一個眾所周知的特性。 它們在圖形中用於創建可縮放的曲線矢量圖形，確保曲線在曲線中移動時保持平滑。 繪製貝塞爾曲線必須知道四個點：起點、終點和兩個控制點。 基於百分比長度路徑的起點和控制點之間的距離用於計算貝塞爾曲線。 對於兩點的中點，將 M 乘以 P0 和 P1。 我幾乎無法像 YouTube 視頻那樣解釋它，所以如果您想了解更多信息，請觀看它。 下面給出了沿貝塞爾曲線求點 P 值的公式。

三個基本測量單位是 P0（點）、P（沿線的點）和 T（沿線的百分比）。 P1 =（未知端點）是找到這個數字的公式。 該比率為 1 – p (t) – 0 / p。

在開始（停止）處與貝塞爾曲線相切的向量垂直於連接前兩個（後兩個）的線。 在開始（停止）處有一個與貝塞爾曲線相切的矢量，但曲線向右傾斜。 不可能用遞歸算法手動生成貝塞爾曲線。 系統從第一個控制點開始，以通過下一個控制點的曲線結束。 它使用簡單，但也可以用來製作任意階的曲線。 通常，曲線從第一個控制點開始。 在第二點，曲線與 y 軸相交。 最後，曲線在第三點與 x 軸相交。 第四個控制點位於曲線與連接前兩個控制點的直線相交的點。 第五個控制點位於曲線與連接第二個和第三個控制點的直線相交的點。 第六個控制點連接第三個和第四個控制點，因為它是曲線與直線相交的點。 第七個控制點是曲線與連接第四個和第五個控制點的直線相交的點。 第八個控制點是曲線與連接第五個和第六個控制點的直線相交的點。 第 9 個控制點是曲線與連接第 6 個和第 7 個控制點的直線相交的點。 當曲線與第七個和第八個控制點的連線相交時，第十個控制點點被定義。 控制點分別位於第十一個和第九個控制點，即曲線與連接第八個和第九個控制點的直線相交的點。 第十二個控制點是曲線與連接第九個和第十個控制點的直線相交的點。 曲線可以按任何順序繪製，但並非所有點在實踐中都有用。 曲線起點和終點的點通常最有用，但它們在曲線的中心也很有用。 貝塞爾曲線算法簡單明了，但您可以使用它來創建任何形狀。

如何在 Svg 中繪製曲線？

要在 svg 中繪製曲線，您需要創建一個元素並在其上定義 ad 屬性。 d 屬性定義元素的路徑數據。 路徑數據由一系列命令和參數組成。 每個命令由一個字母和一個數字組成。 字母代表命令，數字代表參數。 繪製曲線的命令有 C、c、S、s、Q、q、T、t、A、a。 C 命令代表“絕對三次貝塞爾曲線”。 c 命令代表“相對三次貝塞爾曲線”。 S 命令代表“絕對平滑三次貝塞爾曲線”。 s 命令代表“相對平滑的三次貝塞爾曲線”。 Q 命令代表“絕對二次貝塞爾曲線”。 q 命令代表“相對二次貝塞爾曲線”。 T 命令代表“絕對平滑二次貝塞爾曲線”。 t 命令代表“相對平滑的二次貝塞爾曲線”。 A命令代表“絕對橢圓弧”。 a 命令代表“相對橢圓弧”。 這些命令中的每一個都有一組不同的參數來定義曲線。

三次貝塞爾曲線命令（C）如下：[code type=html]。 =1, =1, =1, =1, =1, =1, =1, =1, =1, =1, =1, =1, =1, =1 曲線從點 100,200 開始，路徑前進的地方。 第二個控制點是 400,100。 曲線最後的值為 400,200。 曲線和直線一樣，不必連續彎曲。 如果將一條曲線連接到另一條曲線，則可以創建更複雜的曲線。 瀏覽器使用這些命令（也稱為 S 和 S）來讓您更輕鬆地找到所需內容。

這一次，兩條曲線使用絕對快捷方式表示。 要使用二次貝塞爾曲線，需要一個控制點而不是兩個。 使用 arc 命令，會考慮最多的參數。 曲線命令分為三種類型。 一個起點和終點，一個rx、ry、x軸旋轉的橢圓，四個圓弧都是可能的。 弧用於在掃旗圖像中鏡像大弧旗圖像。 藍色圓弧表示當兩端指向同一方向時圍繞軸形成的紅色圓弧。

因此，值為 0 表示應使用較小的弧，而值為 1 表示應使用較大的弧。 路徑比基本形狀更大、更強大。 它們可以通過更多的努力來創建，但不是很多。 您很有可能所有圖形編輯器都會將圖像導出為路徑。 最好在幾分鐘內記住這些命令。

了解如何在 Svg 中創建路徑

使用 SVG 中的路徑，您可以創建各種形狀，包括圓形和曲線。 在本文中，我們將研究如何使用這些命令來創建這些路由。
A 命令可用於在 SVG 中創建圓弧。 打開圓弧命令窗口後，您將能夠指定將用於生成圓弧的圓或橢圓的 x 和 y 半徑。 您還可以包括圓弧的起點和終點以及繪製圓弧的角度。
C 命令也允許您創建曲線路徑。 如果使用它，它會指定必須繪製的路徑，以及元素 glyph 和 missingglyph。 路徑定義是路徑命令的列表，其中每個命令由一個命令字母和一個代表其參數的數字表示。
例如，要使 SVG 中的路徑居中，您可以使用 viewBox 屬性。 無論它在文檔中的什麼位置，它都會將路徑置於視口的中心。

Svg 貝塞爾曲線生成器

網上有許多 svg 貝塞爾曲線生成器。 這些生成器允許您根據指定的參數創建自定義 svg 貝塞爾曲線。 您可以控製曲線的寬度、高度、控制點數和其他方面。 這些生成器是為您的 Web 項目創建自定義形狀和設計的好方法。

Svg 路徑曲線

SVG 路徑曲線用於在 SVG 路徑上創建平滑曲線。 有四種類型的曲線可用：二次曲線、三次曲線、圓弧曲線和平滑曲線。 每種類型的曲線都有其自身的優點和缺點，因此為手頭的任務選擇正確的曲線類型非常重要。 二次曲線是最簡單的曲線類型，易於創建和操作。 三次曲線更複雜，可用於創建更詳細的形狀。 弧形曲線最適合創建圓形或橢圓形。 平滑曲線是其他三種曲線的組合，可用於創建各種形狀。

路徑是對象輪廓的幾何形狀，它是通過將對象的形狀移動到一側、lineto、curveto（立方和二次斜率）、弧和 closepaths 來定義的。 複合路徑（即具有多個子路徑的路徑）可用於允許對象具有甜甜圈孔。 它描述了SVG 路徑的語法、行為和 DOM 接口以及它們的表達方式。 路徑數據序列中的每個命令都跟在一個字符之後。 路徑數據的語法簡潔，可以實現最小的文件大小，同時還可以實現高效下載。 路徑數據可以分解成多行以提高其可讀性，因為其中的字符包含換行符。 通過在標記中利用規範化的空格字符，屬性名稱中的新行將被規範化。

該值表示路徑數據字符串指定的形狀。 字符串中的錯誤根據路徑數據的路徑數據錯誤處理部分進行處理。 路徑數據段（如果有的話）必須以 moveto 命令（如果有的話）開始。 自動從當前點到當前子路徑的起點繪製直線。 該路徑段可能沒有任何長度。 Closepath 被定義為一條路徑，該路徑由初始段的起點在最終段的末尾使用值'stroke-linejoin'連接。 當第一個和最後一個路徑段未連接時，封閉子路徑和開放子路徑之間存在差異。

Python 目前不支持將段完成關閉路徑操作作為命令。 要更改參考點，一行命令可以從一個點到下一個點繪製直線。 當使用相對 l 命令生成直線時，終點為 (cpy x)。 要在正 x 軸方向繪製水平線，請使用具有正 x 值的相對 h 命令。 前五個示例演示了貝塞爾路徑的單個立方段。 按降序排列，您可以命令橢圓弧。 如果使用相對命令，則圓弧由坐標 (cxy) 表示。

大旗和掃旗表示繪製的弧線數，如下圖所示。 EBNF 處理必須消耗盡可能多的給定產品，以便在字符不再滿足該產品的要求時停止。 當 d 屬性的值為零時，渲染被禁用。 在段邊界處計算封口形狀和顯示標記時，會為段邊界啟用覆蓋。 如果 rx 和 ry 都為零，則此弧將被視為直線段（連接端點的線）。 有關此縮放操作的更多信息，請參閱數學公式的附錄部分。 長度為零的路徑段並不是無效的，它們會在以下情況下對渲染產生影響。

通過向路徑添加“pathLength”屬性，作者可以計算路徑的總長度，以便用戶代理可以計算沿路徑的距離。 “路徑”元素內的移動操作可被視為零長度操作。 只有少數直線、曲線和箭頭可用於計算路徑長度。

路徑、曲線和圓弧：路徑元素的基礎知識

路徑通常使用“線”元素定義，並且可以使用它們創建直線。 此外，'curve' 元素可用於使用'fill' 或'stroke' 元素填充曲線。
如果你想創建一條經過幾個不同點的路徑，你可以使用'arc'元素。 'arc' 元素有兩個特徵：起點和終點。 圓弧的大小也可以通過指定其半徑來指定。
最後，形狀可用於創建路徑。 “路徑”元素有兩個元素：起點和終點。 degree 屬性，也稱為 ad 元素，作為路徑元素的一部分包含在內。 此處指定路徑圍繞形狀的移動程度。
因此，有多種使用路徑的方法，其所有組件都匯總在“路徑”元素中。 因為路徑元素包含一個屬性，即“d”屬性，它告訴它要繪製什麼形狀，請務必記住它包含一個屬性。

Svg 路徑示例

SVG 路徑將對象的形狀定義為一系列相連的直線和曲線。 svg 路徑示例定義了一顆心的形狀。

路徑元素是繪圖中的最後一個元素。 需要 d 屬性來描述它繪製的內容。 它有很多功能，但它主要只是一個迷你語法，具有易於識別的難以理解的值。 我們可以重新格式化代碼以理解它（它仍然具有原始字符）。 路徑可用於繪製一條直線回到設置筆的點，使其成為一種便宜且簡單的方法。 該路徑必須像任何其他命令一樣由 Z（或 z，無所謂）關閉，並且它是一個可選命令。 到目前為止，A 命令是最困難的。 要確定橢圓的寬度、高度和旋轉角度，您需要指定預期採用的路徑。 路徑有兩個可能的橢圓，每個橢圓有兩條不同的路徑，每個橢圓有四個不同的路徑。

三次貝塞爾曲線

三次貝塞爾曲線是計算機圖形學和相關領域中經常使用的參數曲線。 曲線由四個點定義：兩個端點和兩個控制點。 貝塞爾曲線可以組合形成貝塞爾樣條，這是一種分段定義的曲線，由多條端到端連接的貝塞爾曲線組成。

了解貝塞爾曲線背後的數學原理及其與本視頻中其他計時函數的關係。 您可以使用交互式可視化自定義您的可視化，以反映這些美麗過渡背後的數學原理。 曲線是一種特殊類型的曲線，可以用來描繪從一個狀態移動到下一個狀態的過程。 我們現在可以在軸 P0 -> P1 以及 P1 -> P2 上的線段之間連續移動。 如果我們將這兩個點與一段連接起來並在其上放置一個插值點（藍點），則可以獲得類似於二次貝塞爾曲線的路徑。 它被稱為線性插值。 從控制點 P0、P1、P2 和 P3 開始，我們將使用公式來表示立方貝塞爾曲線。

當我們將第四個點 - P4 - 添加到連接這四個點的每個線段時，我們會在線段之間得到一個插值點。 因此，我們鏈接這些點並為每個新線段（綠色）創建一個 (*) 插值 (*) 點。 下一步是連接點並繪製每個點的線段。 最後，我們有一個繪製曲線的公式。 以下是立方體貝塞爾公式的一些表達方式。 ( P0, P1, P2, P3) = for (設 t = 0, t = 1 <= 1); t = 1 換句話說，等式有 1 為 60.res。

推 ( x: valX, y: valY ); 水庫坐標P1和P2代表一個元素的運動，當它過渡時，它遵循這條曲線。 這就是數學概念如何轉化為運動。 使用具有特定立方體貝塞爾過渡的特定曲線可用於表示各種緩動過渡。 為了方便起見，所有這些計時功能都由 CSS 提供。 Framer Motion 發現過渡對像中的 easing 和 immigrate 函數之間存在很強的關係。 Framing Motion 中的 cubic- bezier 函數與我們在 CSS 中看到的有很大不同。

您的 P1 和 P2 點的值必須分別傳遞給 ease 屬性以描述此過渡。 這篇博文為您提供了一些有趣的見解，讓您了解我們每天使用的一些很酷的東西，我希望它能激起您的興趣。 隨著對三次貝塞爾函數和說明的更多了解，您將能夠輕鬆創建新的過渡和動畫。